앞서 '양자역학 이야기 – 드브로이 물질파'에서 우리는 세상을 구성하는 요소들이 입자 뿐만 아니라 파동으로도 이루어져 있다는 것을 배웠다. 기존의 사유 방식으로는 쉽게 납득할 수 없는 개념이지만, 입자라고만 생각되었던 전자의 움직임이 파동의 특성을 보일 수 있음을 수학적으로 유도했고 이것을 물질파(matter wave)라고 부르게 된 것이다.

오늘은 양자역학에서 전자의 존재를 파동으로 설명한 또 다른 유명한 이론인 '파동함수'에 대해서 살펴보고자 한다. 양자역학에 조금이라도 관심이 있었다면, 한 번 정도는 들어봤을 법한 이름 '슈뢰딩거'가 바로 이 이론의 주인공이다.

슈뢰딩거의 고양이

▲ 슈뢰딩거 (출처: 위키백과)

에르빈 슈뢰딩거(Erwin Schrödinger, 1887~1961))는 오스트리아의 물리학자로 드브로이의 물질파 개념에 영향을 받아 '파동방정식'과 '파동함수'를 제안했다.

하지만 보통은 그의 방정식보다 머릿속 상상 실험인 '슈뢰딩거의 고양이'가 더 친숙하다. 이 실험은 슈뢰딩거가 물리학자 보어와 하이젠베르크 중심의 '코펜하겐 해석'을 반박하기 위함이었다. 코펜하겐 해석은 이 세상을 거시세계와 미시세계로 나눈다. 거시세계와 달리 미시세계에서 전자는 입자이기도 하고 파동이기도 한 '중첩상태'에 있다고 주장한다. 상태의 결정은 관찰(측정) 여부에 따라서 정해진다는 일종의 사후 결정론적인 입장을 취한다.

하지만 슈뢰딩거는 그런 일은 있을 수 없다고 하며, 아래와 같은 실험을 상상해 보라고 했다.

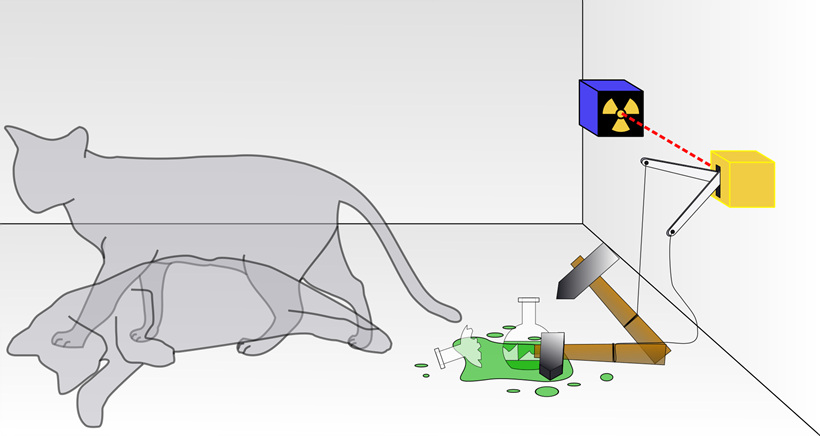▲ 슈뢰딩거의 고양이, 양자역학의 불완전함을 보이기 위해서 고안한 상상 실험 (출처: 위키백과)

이 실험에는 원자와 고양이 한 마리가 등장한다. 고양이는 보이지 않는 상자 속에 들어있고, 원자는 A상태일 수도 있고 B 상태일 수도 있다. 원자가 A상태라면 그림 속 기계장치는 움직이지 않지만, 원자가 B 상태라면 기계가 움직여 독약이 든 병을 깬다. 그리고 고양이는 숨을 거둘 것이다. 그렇다면 원자가 현재 A, B 중에 결정되지 않은 중첩상태라고 가정한다면, 상자 속 고양이는 살아있는 것인가 아니면 죽어있는 것인가? 고양이는 거시세계의 존재인데, 중첩을 주장한 코펜하겐 해석은 어떻게 받아들여야 하는가?

아직 슈뢰딩거 고양이의 역설은 완전히 해결되지는 않았다. 일부 이를 설명할 이론들이 있기는 하지만 명확하지는 않다. 하지만 이러한 문제를 일으키는 원인인 미시세계와 거시세계의 경계가 어디쯤인지 알기 위한 탐구는 분자를 이용한 실험 등을 통해 계속 되고 있다.

하이젠베르크의 행렬역학에 냉소적인 슈뢰딩거

하이젠베르크는 양자역학 연구를 함께 했던 보어와 원자 모델에 대해서는 의견이 달랐다. 그는 양자화 개념을 도입하면서 빛의 세기 해석과 함께 불확실성 원리를 정의하고, 이를 통해 전자구름 모델과 같은 확률분포를 제시했다. 그런 그는 원자의 특성을 파동으로 시도하려는 기존 연구방향을 거부하고, 원자의 에너지 준위를 숫자로만 생각하여 전자 궤도라는 개념을 파괴했다. 이를 통해 수학에 능했던 하이젠베르크는 행렬역학이라는 물리학에서는 낯선 방식으로 양자의 원리를 설명했다.

반면 당시 경쟁자 구도를 그렸던 슈뢰딩거는 하이젠베르크의 수식만 난무한 논문과 그의 설명을 경멸했다. 즉, 하이젠베르크가 내놓은 결과는 오직 숫자로만 관념화될 뿐, 눈에 보이는 그림으로 설명가능한 개념이 아니었기 때문이다. 사실 전자의 구름분포 형태의 시각화도 하이젠베르크의 작품은 아니었고, 후대에 그의 전자 존재에 관한 확률밀도를 해석하는 과정에서 나온 산물이다.

슈뢰딩거는 그림도 없고, 수식만 가득한 하이젠베르크의 이론을 마음이 깃들지 않은 역학이라고 평가절하했다. 이에 슈뢰딩거는 양자역학의 시각화를 위해 파동역학을 새롭게 등장시켰고, 기존의 파동함수를 이용해 에너지의 불연속과 전자의 전이를 설명하고자 노력했다. 그는 보어의 원자모형을 바탕으로 드브로이의 물질파 개념까지 설명 가능한 미시세계의 운동방정식을 만들어 낸 것이다.

슈뢰딩거의 파동함수 의미

슈뢰딩거는 전자가 지닌 파동을 드브로이의 개념인 물질파로 보았다. 파동량이 입자 자체의 밀도라고 해석했던 드브로이의 생각은 물리학자 보른에 의해 조금 개선되었는데 파동량의 제곱이 해당 시공간에서 입자를 발견할 확률진폭이라고 보았다. 슈뢰딩거는 드브로이의 물질파 개념과 보른의 해석을 덧붙여 그만의 파동함수를 이끌어 냈다. 자세한 수식 도출을 하기는 어려우니 수식 모양이라도 보고 가는 것이 좋겠다.

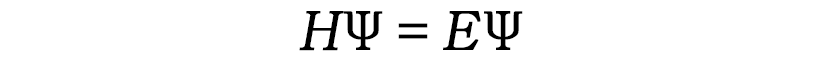▲ 슈뢰딩거의 파동 함수 (Ψ, 그리스어: 프시)

파동함수의 의미를 한 마디로 정의하자면, 물질을 구성하는 입자 또는 파동의 위치 상태를 확률적으로 표현한 함수다. 정확히 말하면 특정한 시간에 특정한 위치에서 입자를 발견할 확률적 크기다.

재미있는 것은 행렬역학이라는 수식만으로 설명한 하이젠베르크나, 눈에 보이는 파동의 모양을 생각하면서 해석한 슈뢰딩거나 똑 같은 결과를 나타낸다는 것이다. 관점이 달랐을 뿐 둘은 한 목소리로 양자의 불연속성을 설명해 냈다.

파동방정식으로부터 도출한 파동함수

슈뢰딩거는 파동함수를 발표하기 전에 먼저 파동방정식을 만들어냈다. 파동방정식은 정의하는 과정에서 운동량, 위치량, 에너지 등을 매개하는 다양한 연산자가 등장하며, 이를 오퍼레이터(Operator)라고 부른다. 파동방정식은 다양한 연산자와 결합하면서 굉장히 단순한 파동함수로 표현할 수 있게 된다.

▲ 다양한 연산자들

슈뢰딩거의 파동함수는 표현이 단순했으나 보어의 원자모델을 설명하기에 충분했으며, 하이젠베르크의 확률분포 해석과도 상응하는 결과를 낳는다. 또한, 개별 전자궤도내에 존재하는 전자의 파동은 고유값(E1, E2, E3 등)을 지니면서 양자화가 된다. 전자의 움직임이 슈뢰딩거 파동방정식을 만족시킬 때 양자화가 되는 것이다.

전자가 존재하는 영역에 대해 하이젠베르크는 불확실성의 원리를 통해 확률분포라는 개념으로 위치를 제한하였고, 슈뢰딩거는 파동방정식과 파동함수를 통해 전자가 궤적이 아닌 확률이라는 개념에 한 발짝 더 다가서게 했다. 슈뢰딩거의 파동함수는 이후 양자역학에서 전자의 확률 구름모델에 힘을 더해주는데 기여했다.