양자역학은 빛이 입자인지 파동인지를 놓고 본격적으로 시작됐다. 하지만 당시 과학자들의 생각과 달리 빛은 입자성과 파동성을 모두 갖는다는 이중성으로 결론을 맺었다. 빛의 입자가 파동처럼 움직이는 것이 아니다. 입자이면서 파동인 것이다. 우리의 직관으로는 납득하기 어려운 개념이지만 과학적 결론은 그렇다.
그리고 여기 직관적으로는 납득하기 어려운 또 하나의 이론이 있다. '드브로이 물질파'. 빛만 이중성이 있는 것이 아니라, 물질에도 이중성이 있다는 이 이론은 어떻게 등장했으며, 양자역학에 어떤 기여를 했을까?
물질의 이중성을 파헤치다
루이스 드브로이(Louis de Broglie, 1892~1987)는 프랑스 귀족 가문 출신이었다. 그는 아인슈타인이 빛이 입자라고 1905년 제안한 '광양자설'과 이를 실험적으로 검증한 1923년 콤프턴 효과에 큰 관심을 가졌다. 드브로이는 빛이 입자성과 파동성이라는 두 가지 성질을 모두 갖고 있다는 데에 착안해, 물질도 이중성을 갖고 있다는 가설을 1924년 박사학위 논문으로 제안한다.
기존의 상식으로 물질은 당연히 입자라고 여겼기 때문에 그의 가설은 말도 안 되는 발상으로 여겨졌다. 그의 지도교수였던 물리학자 폴 랑주뱅은 이 논문에 대해 아인슈타인에게 자문을 구했고, 아인슈타인은 "이 연구는 물리학에 드리운 커다란 베일을 걷어냈다."라는 찬사를 보냈다. 물질의 이중성이 드디어 밝혀지기 시작한 것이다.
드브로이 물질파란?
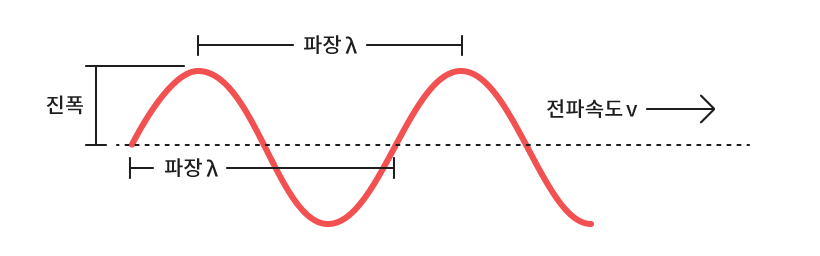
▲ 파동의 기본적인 구성요소
입자와 파동은 서로 공통점을 찾을 수 없는 개념이다. 입자는 당연하게도 질량이 있다. 위치가 정해질 수 있고, 움직이기도 하므로 속도라는 개념도 있다. 즉 운동량이라는 개념이 존재한다. 반면 파동은 파장, 진동수, 진폭과 같은 입자와는 전혀 다른 개념으로 표현된다. 드브로이는 이러한 전혀 상반된 두 가지 개념을 물질, 조금 더 정확히 말하면 물질을 구성하는 원자 속 전자가 갖는다고 생각했다.
그는 아인슈타인의 특수상대성이론 중 에너지=질량 공식(E=mc²)과 광양자 가설, 플랑크의 에너지 양자 가설에서 영감을 얻었다. 물질의 질량이 곧 에너지이고, 파동에도 에너지가 있으므로 에너지를 중심으로 이들의 관계식을 결합해 질량이 파동적 성질을 갖고 있다는 새로운 결론을 도출했다. 즉, 입자라고만 생각되었던 전자의 움직임이 파동의 특성을 보일 수 있음을 수학적으로 유도했고 이것을 물질파(matter wave)라고 부른다.
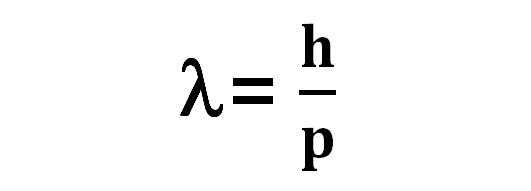
λ(파장), h(플랑크상수), p(운동량)
▲ 드브로이 물질파 공식
수학적 유도를 최대한 간단히 표현하자면, E=mc2=pc(운동량-에너지 관계식)에서 E(에너지)는 pc(운동량)으로 변환된다. 이를 E=hn=hc/λ(광전자효과 관계식)과 결합시키면 pc=hc/λ이 도출된다. 양쪽의 항에서 c(빛의 속도 상수)를 모두 소거하면 p=h/λ이 되고 최종적으로 드브로이 물질파 공식 λ=h/p가 도출된다. 드브로이는 모든 입자에서도 λ(파장)은 h/p(플랑크 상수를 운동량으로 나눈 값)으로 표현할 수 있다고 생각했다. 즉, 모든 입자는 파장의 특성을 지닌다는 것으로, 전혀 다른 성질의 두 개념을 하나의 방정식으로 묶는 데 성공했다.
물질파 개념, 보어의 원자 모델을 완성하다
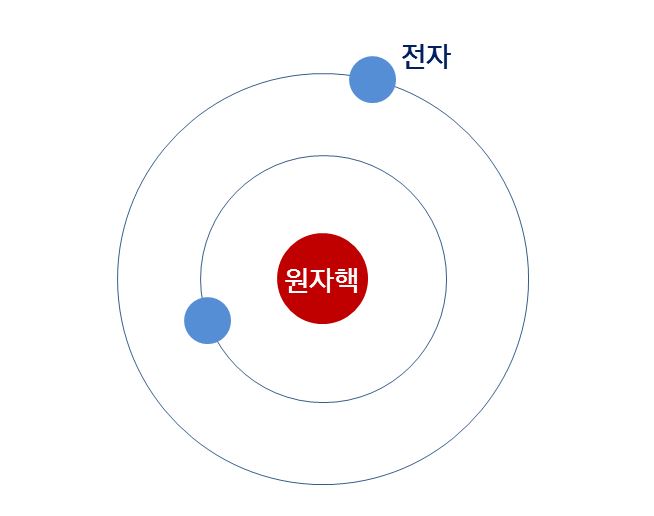
▲ 보어의 원자 모형
보어의 원자 모형에 대해서 다시 떠올려보자. 보어의 원자 모형은 원자핵이 중심에 있고, 전자가 그 주위의 궤도를 도는 모습이다. 태양계의 모습과 비슷하다. 그런데 보어의 원자 모형을 설명하는 데에는 해소되지 않는 의문이 있었다. 전자가 원자핵의 인력에 끌려가 충돌해 소멸하지 않고 계속 공전을 하는 이유와 전자가 궤도를 순간적으로 이동한다는 설명에는 근거가 부족했다. 보어는 이를 양자 조건이라는 가정으로 근거를 모호하기 제시했기 때문이다.
물질파는 이러한 보어의 원자 모형을 설명하는데 탁월했다. 물질파는 다른 종류의 파동과 동일하게 행동한다. 드브로이는 보어의 모형에서 전자의 궤도가 전자파동의 정상파(standing wave)로부터 자연적으로 도출된다고 보았다.
정상파란,
기타의 현의 울림과 같이, 진동의 마디 위치가 묶여 있는 양끝을 기준으로 현의 내부에서만 움직이는 것을 말한다. 즉 묶여있는 또는 멈춰있는 파를 지칭한다.
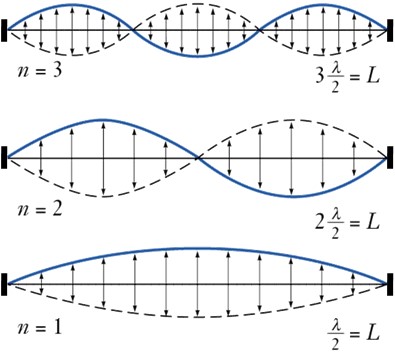
▲ 1차원 모델내 정상파 (원자 내부의 n 궤도를 돌고 있는 전자가 가질 수 있는 정상파로, 좌우 양 끝을 원형으로 이어 붙이면 아래와 같이 진동하는 궤도 형태가 된다.)
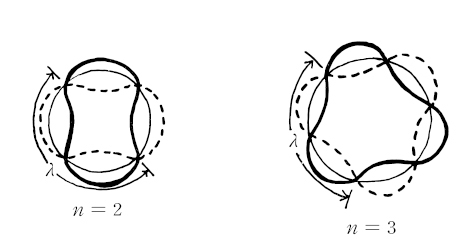
반대로 파동이 정수배의 파장 조건을 갖추지 못하면 상쇄간섭 때문에 소멸하게 되는데, 이럴 경우 전자가 존재하지 않는 궤도가 된다. 따라서 전자의 궤도가 띄엄띄엄 있는 이유가 물질파의 보강간섭을 일으키는 정상파만이 존재하기 때문이라는 설명이 가능해졌고, 보어의 양자 조건은 더 이상 모호한 가설이 아닌 현실이 되었다.
드브로이 가설의 실험적 검증
입자를 동반하는 파동인 물질파는 우연히 검증되었다. 1924년 물질파의 개념이 나왔지만, 드브로이의 가설을 전혀 모르는 상태에서 진행한 두 과학자의 실험이 물질파의 존재를 입증했다.
데이비슨(Clinton Davission, 1881-1958)과 저머(Lester Germer, 1896-1971)는 당시 웨스턴 일렉트릭사(Western Electric Company, 추후에는 Bell Telephone Laboratories)의 진공관에 관한 특허분쟁 문제를 해결하고자 니켈 단결정을 이용한 전자 산란 실험을 실시하였다. 전자가 입자라는 가정을 버리고 파동으로 해석했을 때, 즉 브래그(William Bragg, 1862-1942) 방정식(nλ=2dsinθ)으로 계산했을 때 특허 문제를 해결할 실험결과가 설명된다는 것을 발견했다. 그들은 이후에 영국과학회에서 드브로이의 물질파 이론을 듣고 실험결과의 이론적 토대를 찾았으며, 드브로이의 물질파의 존재를 실험적으로 증명(1927년)했다.
그로부터 1년뒤 물리학자 톰슨(George Thompson, 1892-1975)은 X-선과 동일한 파장을 지닌 전자에 의한 두 가지 회절의 모양이 거의 일치한다는 실험을 통해 다시 한 번 전자의 물질파 특성을 증명하게 된다. 광자(빛)과 전자(물질)에서 동일한 현상이 발견된 것이다.
다양한 물질파
물질파 개념에 의하면 움직이는 모든 입자는 파동의 성질을 지닌다. 그렇다면 투수가 던진 야구공도 파동이 될 수 있을까?
질량이 150g인 야구공을 40m/s로 던졌을 때 가질 수 있는 물질파의 파장은, h/mv 공식에 의해 1.1×10-34 m가 된다. 숫자를 보면 알겠지만 원자 단위의 너무 작은 파장이다. 사람이나 웬만한 측정기구로는 감지할 수 없다. 다른 예를 들면, 지구가 공전하면서 발생하는 물질파의 파장은 10-52nm, 날아가는 골프공은 10-23nm의 파장을 지닌다. 이것도 역시 알아챌 수 없다. 거시세계에서의 입자는 발생되는 물질파의 파장 크기가 인지할 수 없을 정도로 작기 때문에 드브로이의 물질파는 무시된다.
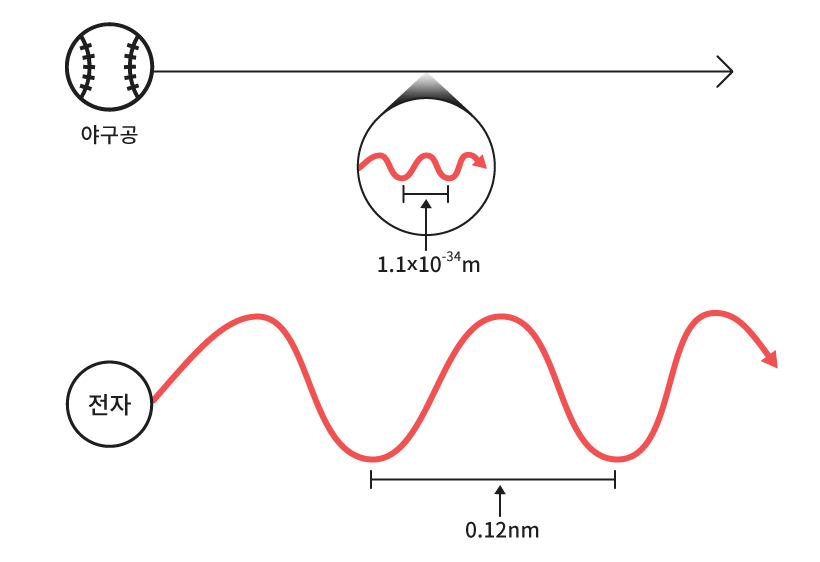
그러나 100V로 가속된 전자(5.9×106 m/s, 9.11×10-31 kg)가 지닐 수 있는 파장은 0.12 nm가 된다. 이것도 무척 작은 값이지만, 원자의 세계에서 보면 결코 작지 않다. 이 파장은 390 nm 정도로, 가장 짧은 가시광선 보다 더 짧다. 따라서 미시 세계에서 물질파는 큰 의미를 갖는 반면, 거시 세계의 일반적인 물체는 빛의 속도로 달리지 않는 이상 물질파의 특성을 관찰하기 힘들다고 봐야 한다.
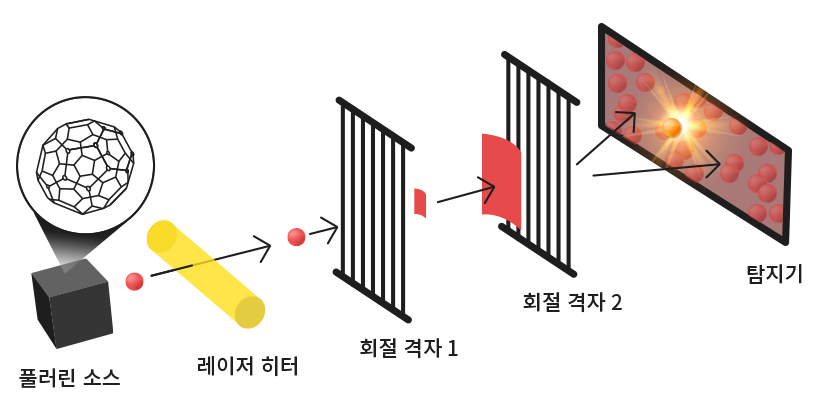▲ 플러렌을 이용한 물질파 검증 실험
직접 눈으로 볼 수 없는 전자를 파동으로 볼 수 있다고 하는 개념은 그렇다 치고, 관측 가능한 입자의 수준에서도 정말로 파동의 특성이 그대로 나타날 것인가는 최근 실험결과로 확인됐다. 플러렌(C60)은 약 1nm 정도의 크기를 지닌 탄소로 된 결정체로, 플러렌을 레이저히터를 통과시킨 뒤 회절격자 패턴을 통과시키는 실험을 했다. 이때 검출기에 나타난 결과는 영의 이중슬릿 실험과 일치하는 것으로 파동성을 그대로 나타냈다. 이로서 우리가 직관적으로 입자라고 생각하는 물질에서도 파동성이 증명됐다.
양자의 세계에서 벌어지는 일들은 과학적으로 검증되고 있음에도 불구하고, 아직 우리가 직관적으로 받아들이기 힘든 경우가 많다. 하지만 천동설이 지동설로 바뀌는 등 과학적 패러다임 변화 속에서 우리의 고정관념이 사라졌듯이, 양자역학의 개념도 이해하게 될 것으로 예상한다.
