
우리는 은행을 통해 돈을 이체하거나 환전하려면 수수료를 내야 한다. 심지어 거래하고 있는 은행의 내 돈을 다른 은행이 운영하는 ATM 기기를 이용하여 찾을 때도 비싼 수수료를 낸다. 반면 비트코인과 같은 가상화폐는 은행이나 환전소를 거치지 않고 당사자들끼리 직거래하기에 수수료가 낮거나 없다는 장점이 있다. 하지만 사이버 세계에서 직거래는 상품값은 치렀으나 상품을 보내주지 않는 것과 같은 사고와 사기의 위험이 따라서 가상화폐로 거래를 할 때는 반드시 거래에 대한 신뢰가 필요하다. 그렇다면 가상화폐를 암호화하는 방법에는 어떤 것이 있는지 알아보자.
정보를 암호화하는 두 가지 방법

컴퓨터와 같은 전자기기를 이용한 통신 환경은 허락받지 않은 공격자가 통신 중인 정보를 도청하여 변조하거나 다른 내용을 삽입 또는 삭제할 수 있다. 이런 문제점을 해결하는 가장 안전한 방법은 정보를 암호화하는 것이다. 암호화된 정보를 원래대로 되돌리는 것을 ‘복호(複號)’라고 한다. 반면, 우리가 보통 암호의 내용이 무엇인지 밝히는 것을 ‘해독(解讀)’이라고 하는데 해독은 중간에 정상적이지 않은 과정으로 암호문의 내용을 알아내는 것을 뜻한다. 정보를 암호화하는 방법은 크게 ‘비밀열쇠방식’과 ‘공개열쇠방식’이 있다.
비밀열쇠방식은 보내고자 하는 정보를 암호화할 때, 암호화하는 열쇠와 복호하는 열쇠가 서로 대칭이다. 즉, 정보를 보내는 쪽이나 받는 쪽 중에서 하나의 열쇠만 알면 다른 쪽의 열쇠를 알 수 있다. 예를 들어 a라는 정보를 보낼 때, 정보를 보내는 송신자는 a를 암호화하기 위하여 a에 3을 더하여 a+3을 만들었다면 송신자의 암호 열쇠는 (+3)이다. 또 정보 a를 받는 수신자는 a+3을 받았으므로 이것을 복호하려면 여기에 3을 빼야 한다. 그래서 (a+3)-3=a라는 정보를 받는다. 즉, 수신자의 복호 열쇠는 송신자의 암호 열쇠 (+3)의 음수인 -3이다. 여기서 송신자의 암호화 열쇠가 공개되면 수신자의 복호 열쇠도 바로 알 수 있기에 정보는 안전하게 보호되지 못한다.
불과 몇 십 년 전까지만 해도 사용되었던 비밀열쇠방식은 특히 전쟁에서 매우 유용하게 사용되었다. 유사 이래 여러 나라가 한꺼번에 참여했던 두 번의 세계 대전 중에서 2차 세계 대전은 본격적으로 암호를 사용했던 전쟁이다. 제2차 세계 대전 중에 독일군은 에니그마(Enigma)라는 기계를 이용한 암호로 연합군 측에게 막대한 피해를 주었다. 그래서 연합군 측에서는 독일의 암호를 해독하기 위하여 많은 전문가를 동원했고, 그 가운데 수학자 앨런 튜링은 에니그마의 암호화 과정을 역으로 추적할 수 있는 ‘폭탄(Bomb)’이라는 이름의 암호 해독기를 개발했다. 그래서 연합군은 독일군의 지상 병력뿐만 아니라 대서양에서 활개를 치던 U보트의 활동 상황까지 낱낱이 파악할 수 있게 되었다. 또 연합군의 노르망디 상륙 작전을 성공으로 이끄는 결정적인 역할로 세계 대전의 전세를 완전히 뒤집었다.
암호의 오래된 역사
오래된 암호 가운데 가장 잘 알려진 비밀열쇠방식은 카이사르 암호(Caesar cipher)로 간단한 치환 암호의 일종이다. 즉, 암호화하고자 하는 내용을 알파벳별로 일정한 거리만큼 밀어서 다른 알파벳으로 치환하는 방식이다.
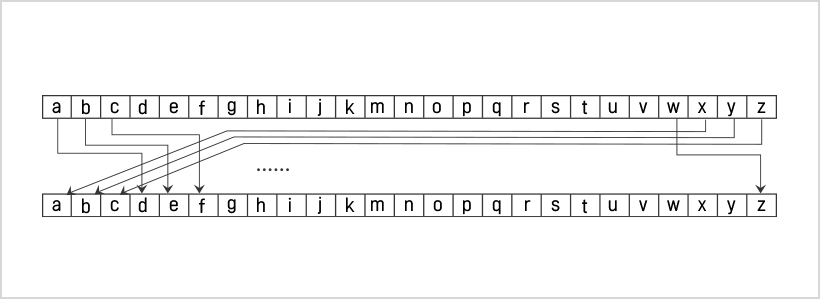
▲ 카이사르 암호는 각각의 알파벳을 일정한 거리만큼 밀어 글자를 치환하는 방식으로 암호화한다.
예를 들어 3글자씩 밀어내는 카이사르 암호를 이용하여 ‘come back home’을 암호화해 보자. 우선 ‘come back home’의 알파벳을 순서대로 늘어놓은 후 세 글자씩 밀어내면 다음과 같이 ‘frphedfnkrpv’가 된다. 이 문장을 원래의 문장으로 바꾸기 위해서는 다시 뒤로 3글자씩 밀면 된다.
그런데 이런 암호는 영어에서 사용되는 알파벳의 사용빈도를 이용하면 비교적 쉽게 해독할 수 있다. 실제로 영어에서는 E가 12.51%, T가 9.25%, A가 8.04%, O가 7.60%, I가 7.26%, N이 7.09%, S가 6.54%, R이 6.12%, H가 5.49% 등으로 사용되고 있다. 따라서 암호문 가운데 가장 많이 사용된 알파벳을 E로 대신하고, 그다음으로 많이 사용된 알파벳을 T로 바꾸면 해독 작업은 한층 수월해진다. 또 영어에서 가장 빈번하게 짝 지어지는 철자는 TH이며, HE, AN, IN, ER 등이 그다음으로 많이 나타난다. 그리고 사용빈도가 가장 높은 짧은 단어들은 THE, OF, AND, TO, A, IN, THAT, IS 순이다. 카이사르 암호는 이런 사실을 바탕으로 해독할 수 있다. 사실 카이사르 암호는 y=x+3인 일차함수와 같다. 주어진 일차함수에 의하면 x에 어떤 값을 대입하면 y는 x보다 3만큼 밀려서 나오게 된다. 따라서 암호도 함수를 이용하여 만들어진다는 것을 알 수 있다.
카이사르 암호는 간단하게 문장을 암호화할 수 있다는 장점이 있지만 긴 문장을 보내면 알파벳의 사용 빈도수를 알기에 해독 가능하다는 단점이 있다. 카이사르 암호보다 해독하기 어려운 것이 스키테일(Scytale) 암호이다.
그리스의 역사학자 플루타르크에 의하면 지금으로부터 약 2,500년 전 그리스의 스파르타에서는 전쟁터에 나가 있는 군대에 비밀메시지를 전할 때 암호를 사용했다고 한다. 이들의 암호 방법은 오늘날의 시각에서 보면 매우 간단하나 그 당시로서는 아무나 쉽게 해독할 수 없는 아주 교묘하고도 획기적인 방법이었다. 스키테일 암호는 다음과 같은 방법으로 암호화한다.

▲ 최초의 암호 장치 스키테일 (출처: 위키피디아)
①전쟁터에 나갈 군대와 본국에 남아있는 정부는 각자 스키테일이라고 하는 굵기가 같은 원통형 막대기를 나누어 갖는다. ②비밀리에 보내야 할 메시지가 생기면, 암호 담당자는 스키테일에 가느다란 양피지 리본을 위에서 아래로 감은 다음 옆으로 메시지를 적는다. 그러면 일정한 간격으로 글자가 써지게 된다. ③리본을 풀어내어 펼친 후 비어 있는 공간에 적당히 글씨를 채워 넣는다. 그러면 메시지의 내용은 아무나 읽을 수 없게 된다. ④이 암호는 오직 같은 굵기의 원통 막대기를 가진 사람만이 메시지를 읽을 수 있다.스키테일 암호는 문자는 그대로 사용하고 위치만 바꾸어 암호화하는 전치암호이다. 일반적으로 많이 사용되고 있는 암호들이 이 전치암호에 바탕을 두고 있기에 전치암호는 현대적인 암호계에서도 중요한 역할을 하고 있다.
소인수분해의 수학적 원리를 활용한 RSA 암호

한편 공개열쇠암호는 암호화 열쇠와 복호 열쇠가 대칭적이지 않은 방식이다. 공개열쇠암호 체계를 이용하고 있는 암호는 대표적으로 ‘RSA 암호’와 ‘타원곡선 암호’ 두 가지가 있다. RSA 암호의 경우 소수인수분해를 이용해 만든 열쇠를 이용하는 방식이다. 이때 사용하는 소수는 몇십 자리, 몇백 자리로 사람들이 알아내기 어렵게 열쇠를 구성한다. 반면 타원곡선 암호는 타원곡선 함수를 이용해 함수 위의 점으로 암호문의 열쇠를 선정하고, 이렇게 만들어진 열쇠를 이용하는 암호 방식이다. 그런데 타원곡선 암호 방식은 타원을 배우지 않은 사람들이 많으므로 여기서는 소개하지 않고, 중학교 수학 시간에 배운 소인수분해를 이용하는 RSA 암호를 간단히 소개한다.
RSA는 1978년에 매사추세츠 공과 대학(MIT)의 리베스트(R. Rivest), 샤미르(A. Shamir), 아델먼(L. Adelman)이 공동으로 개발했기에 그들 이름의 앞 글자를 따서 붙인 이름이다. RSA 암호는 큰 수의 소인수분해에 많은 시간이 필요하나 소인수분해의 결과를 알면 원래의 수는 곱셈으로 간단히 구해지는 사실에 바탕을 두고 있다.
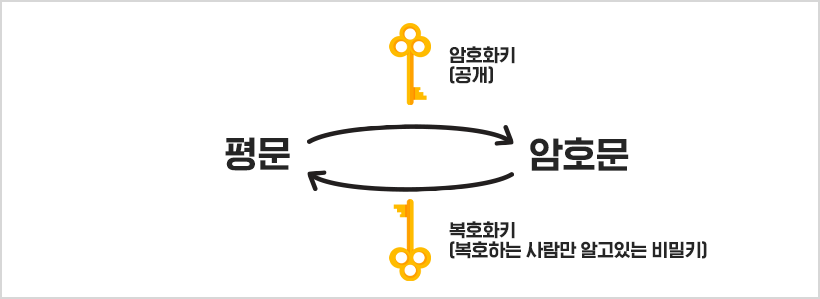
일반적으로 전달하려고 하는 문장이나 식을 평문이라고 하고, 평문을 공개키를 이용하여 암호화한 문장을 암호문이라고 하는데, 기본적으로 다음과 같은 규칙으로 진행된다.
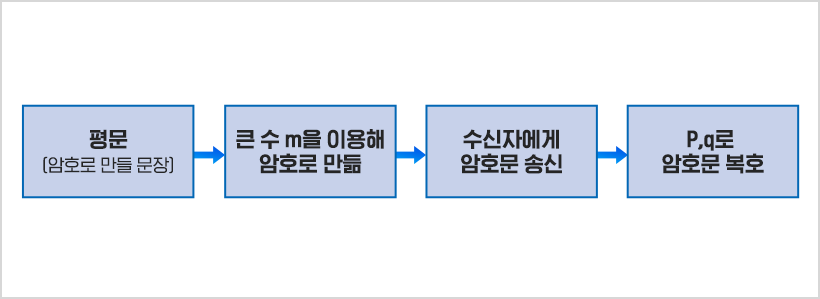
여기서 m은 알려지지 않은 두 소수 p,q의 곱 m=pq이다. 따라서 암호문을 원래의 평문으로 돌리려면 m을 소인수분해하여 p와 q를 구해야 한다. 소인수분해는 어떤 수를 소인수의 곱으로 나타내는 방법으로 순서를 생각하지 않는다면 표현 방법은 유일하다. 이를테면 60을 소인수분해 하면 60=2×2×3×5=22×3×5이다. 소인수분해를 이용하면 RSA 암호는 두 가지 점에서 암호화에 유용하다.
첫 번째 장점은 소수를 찾기 매우 어렵다는 것이다. 주어진 수를 소인수의 곱으로 나타내기 위해서는 어떤 수가 소수인지 알아야 한다. 이를테면 작은 수 13, 17, 19 등은 소수인지 금방 확인할 수 있다. 하지만 약간 큰 수 6700419는 소수일까 아닐까? 이 수가 소수인지 아닌지 알려면 이 수가 1보다 큰 어떤 정수로 나누어 떨어지는지 확인해야 한다. 그러나 이는 시간이 너무 오래 걸리고, 사실 6700419는 소수가 아니다. 두 번째 장점은 주어진 수를 어떤 소수의 곱으로 나타낼 수 있는지 알기 매우 어렵다. 예를 들면, 1837100231809는 두 소수의 곱이라고 가정해보자. 그렇다면 과연 그 두 소수는 무엇일까?
어떤 암호를 만드는 데 두 소스를 곱한 수 1837100231809을 이용했다는 사실을 공개했다고 가정하자. 암호문을 복호하거나 해독하기 위해서는 이 수가 어떤 소수의 곱인지 알아야 한다. 사실 1837100231809=274177×6700417이므로 두 소수는 274177과 6700417이다. 이때 두 소수 274177과 6700417을 곱하여 1837100231809을 구하는 것은 쉽지만, 거꾸로 1837100231809이 어떤 두 소수의 곱으로 되어 있는지 찾는 소인수분해 문제는 매우 어렵다. RSA 암호는 바로 이와 같은 원리를 이용한 것이다. 이런 원리는 마치 들어가기 쉽지만 나오기는 어려운 덫에 설치된 문과 같기에 ‘덫문’이라고도 한다.

0과 1을 동시에 처리해서 방대한 연산을 빠르게 해결할 수 있는 양자 컴퓨터의 등장 이후에는 소수를 이용하는 이 방법이 한계에 직면할지 모른다. 그래서 기술이 발전함에 따라서 쉽게 풀려버릴지도 모르는 현재의 암호화 기술을 보완하고, 양자 컴퓨터를 막아낼 수 있는 양자 암호를 개발해야 하는 과제가 남아있다. 더욱이 거의 일어날 확률은 0이지만, 아무 생각없이 어떤 수를 공개열쇠의 비밀 열쇠로 정하고 계산했더니 암호문이 해독될 수도 있다. 이런 일을 예방하기 위해서라도 일정 기간이 지나면 암호화 열쇠를 바꿔주는 것이 가장 안전하다.
※ 이 칼럼은 해당 필진의 개인적 소견이며 삼성디스플레이 뉴스룸의 입장이나 전략을 담고 있지 않습니다.

