
2020년 1년 동안 매일 빠짐없이 미디어에 오르내리는 주제는 코로나19와 관련한 소식이다. 덕분에 전 국민이 각종 전문 용어에 익숙해지게 됐는데, 그중 하나가 바로 ‘수학적 모델링’ 혹은 ‘수학 모델’이다. 의학이 아닌 수학 용어가 왜 갑자기 튀어나온 걸까. 국내외 학자들이 코로나19의 확산 추세를 분석하고 예측한 결과를 소개하면서 이 용어가 자주 언급됐기 때문이다. 하지만 익숙해진 만큼 수학적 모델링이라는 용어가 무엇이고 어디에 쓰이는지 제대로 아는 사람은 많지 않다.
다양한 분야에서 벌어지는 현상을 수학 언어로 설명하는 ‘수학적 모델링’
언론을 통해 코로나19 확진자 수의 변화를 예측하는 수학적 모델링 연구가 많이 소개되기 때문에 많은 사람이 수학적 모델링을 감염병 연구에 쓰이는 수학적 기법이라고 생각할 수 있다. 하지만 그렇지 않다. 수학적 모델링은 자연과 사회, 기술 등 다양한 분야에서 벌어지는 현상을 수학이라는 언어로 설명하는 것을 말한다.

▲수학적 모델링의 아버지라 할 수 있는 ‘아이작 뉴턴’.
수학적 모델링의 역사는 16~17세기까지 거슬러 올라간다. 수학과 물리학, 천문학이 발전하면서 독일의 요하네스 케플러, 영국의 아이작 뉴턴 같은 학자들이 수학을 이용해 자연 현상, 특히 천체의 운동을 설명하고 예측하기 시작했다. 고등학교에서 배운 미적분학을 이용한 운동방정식이 바로 대표적인 사례다. 아이작 뉴턴은 천체가 운동하는 원리를 자신이 고안한 미분방정식으로 설명했고, 이를 통해 천체의 향후 움직임을 예측할 수 있었다. 이처럼 어떤 현상 혹은 시스템의 작동 원리를 수학적으로 기술하는 것을 수학적 모델링이라고 한다.
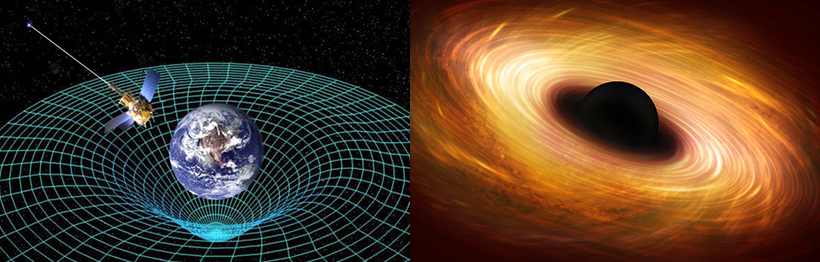
▲아이슈타인은 일반상대성이론을 통해 별과 행성의 중력이 시공간을 휘게 한다고 예언했다. (출처: 위키미디어)
2020년 노벨물리학상의 주인공인 ‘블랙홀’도 수학적 모델링이 낳은 산물이라고 할 수 있다. 올해 노벨물리학상 수상자 중 한 명인 로저 펜로즈 영국 옥스퍼드대 수학과 교수가 알베르트 아인슈타인의 일반상대성이론으로부터 얻은 결론이기 때문이다.
일반상대성이론은 뉴턴의 운동방정식보다 훨씬 정교하게 우주의 천체가 운동하는 원리를 설명하는 수학 모델이다. 즉, 일반상대성이론이라는 수학 모델에서 예측한 결과로 나타나는 현상이 블랙홀인 것이다. 펜로즈 교수는 수학적 모델링을 통해 블랙홀의 존재를 예측했고, 다른 두 사람의 수상자가 실제 망원경을 이용한 천체관측으로 블랙홀의 존재를 확인했다. 스웨덴 노벨상위원회는 이러한 공로를 높이 평가해 세 사람을 노벨물리학상 수상자로 선정했다고 밝혔다.
감염병 연구의 필수품이 된 수학!
뉴턴이 천체의 운동을 수학적으로 설명하고 약 80년이 흐른 18세기에 이르러 감염병 연구에도 수학적 모델링이 도입됐다. 스위스의 수학자이자 물리학자인 다니엘 베르누이가 천연두 확산 과정을 수학적으로 모델링한 것이다. 그는 모델링 결과 예방접종을 할 경우 기대수명이 3년 2개월가량 늘어난다는 예측을 제시하며 백신의 중요성을 강조했다.
본격적으로 전염병을 수학 모델링으로 연구하기 시작한 것은 20세기부터라고 할 수 있다. 영국의 병리학자인 로널드 로스는 1893년 모기의 침샘에서 말라리아 기생충을 발견하고 말라리아의 전파 경로를 수학적으로 밝혔다. 그는 이 연구로 1902년 노벨 생리의학상을 수상했다.
1972년에는 스코틀랜드의 수학자 윌리엄 컬맥과 전염병 학자인 앤더슨 맥켄드릭이 전염병 확산을 설명하고 예측하는 독보적인 수학 모델인 SIR 모델을 제시했다. 이 모델은 현재까지도 코로나19를 비롯해 에볼라, 독감 등 각종 전염병 확산을 연구할 때 기본적으로 활용되고 있다. 또 많은 학자들이 이 모델에서 파생된 다양한 수학 모형으로 전염병 전파 양상을 연구한다.
SIR 모델이 전염병 확산을 예측하는 원리
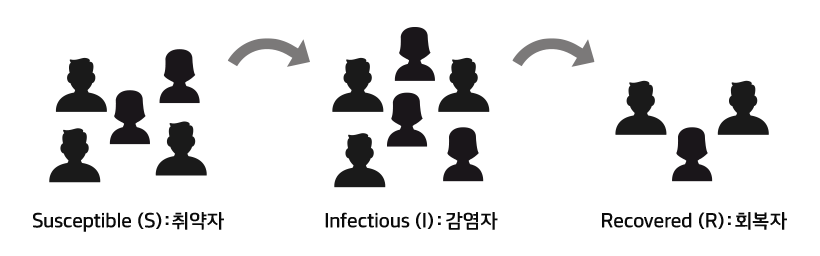
▲SIR 감염확산 모델을 나타낸 그림
SIR 모델이 어떻게 전염병 확산을 예측한다는 걸까? 조금 더 자세히 살펴보자.
SIR 모델은 전염병이 전파되고 있는 지역에 있는 사람을 감염 가능성이 있는 집단(S)과 이미 감염된 집단(I) 그리고 회복된 집단(R)으로 나눠 분석하는 모델이다. 각 집단의 수를 나타내는 수식과 집단과 집단 사이의 상호작용을 나타내는 수식은 모두 미분방정식으로 이뤄져 있다. 감염 집단의 변화에 따라 감염 위험군과 회복군이 시간에 따라 어떻게 달라지는지 계산을 통해 알 수 있다.
특히 감염에 영향을 미치는 거리두기나 접촉과 관련된 요소를 통제했을 때 어떤 변화가 나타나는지 알 수 있기 때문에 전염병 확산을 방지하기 위한 전략을 수립하는 데 활용할 수 있다. 실제로 미국과 유럽에서는 SIR 모델을 발전시킨 전염병 확산 수학 모델을 방역 정책에 활용하고 있다.
한편, 국내 한 수학 연구팀에서도 SIR을 변형한 수학 모델을 이용해 코로나19 전파를 예측하는 연구를 활발히 하고 있는데, 이 연구팀은 SIR에 감염에 노출된 집단(E)과 행동변화라는 변수를 더한 수학 모델을 개발해 코로나19 전파 양상을 분석하고 예측했다. ‘감염에 노출된 집단(E)’은 바이러스에 감염됐으나 잠복기에 있어서 다른 사람에게는 전파하지 않는 집단을 말하며, ‘행동변화’는 마스크 착용, 거리두기와 같은 방역 지침을 적극적으로 따르는지 여부를 나타낸다.
그런 뒤 바이러스 확진자와 완치자, 사망자 관련 통계를 반영해 계산했다. 그 결과 7월 초에는 우리나라 국민의 신종 코로나바이러스 감염 확률이 2월보다 4분의 1가량 낮아졌다는 것을 알 수 있었다. 이는 마스크를 철저히 착용하고 거리두기와 재택근무 등을 하면서 전보다 다른 사람들과의 접촉이 약 4분의 1 수준으로 줄었다는 뜻이다. 하지만 연구팀은 감염 확률을 5.5분의 1 수준으로 낮춰야 코로나19 전파를 억제할 수 있을 것으로 예상했다. 계산 결과 감염 확률이 5분의 1이면 연말에는 매일 400명의 확진자가 나오지만, 5.5분의 1이 되면 환자가 거의 발생하지 않았기 때문이다. 평상시 하루 100명의 사람을 만났고, 7월 초에는 약 25명의 사람을 만났다면 18명 수준으로 줄여야 한다는 뜻이다.
안타깝게도 8월 휴가 등으로 거리두기가 소홀해지면서 수도권을 중심으로 확진자 수가 폭증했다. 확진자 통계를 수학 모델에 반영해 분석한 결과 수도권 시민들이 평상시의 약 40~50% 수준으로 사회활동을 했을 때 이런 결과가 나오는 것으로 나타났다.
디스플레이 연구에도 활용되는 수학 모델

전염병을 중심으로 설명했지만 앞서 밝힌 것처럼 수학 모델은 활용 분야가 광범위하다. 특히 첨단 기술 분야에서도 나타나는 현상의 원리를 설명하고 예측하는 데 수학 모델이 중요한 역할을 한다.
디스플레이 분야에서도 마찬가지다. LCD의 응답 속도는 잔상 현상에 영향을 미치는데, 프랑스 국립과학연구원의 연구진은 수학 모델을 만들어서 이 현상을 설명한 연구 결과를 국제학술지 ‘정보디스플레이협회저널’ 2012년 6월 18일자에 발표했다. 또 중국 칭화대 연구진은 LED 칩의 수명을 예측하기 위해 LED 내부에 생기는 흠이 어떻게 커지는지를 수학 모델로 연구하고 그 결과를 국제 전기·전자기술자협회(IEEE)에서 발행하는 ‘IEEE광학저널’ 2017년 8월호에 발표했다.
코로나19로 인해 갑작스럽게 수학적 모델링 혹은 수학 모델이 대중의 주목을 받게 됐지만 사실 우리는 이미 수학 모델의 영향력 속에 살아가고 있다. 의학과 공학, 자연과학은 물론 심지어 사회과학에 이르기까지 수많은 분야가 수학 모델의 힘을 빌려 발전하고 있기 때문이다.
※ 이 칼럼은 해당 필진의 개인적 소견이며 삼성디스플레이 뉴스룸의 입장이나 전략을 담고 있지 않습니다.

