무시무시한 위력을 지닌 태풍 여러 개가 우리나라에 큰 피해를 주며 지나간 자리에는 어느덧 고추잠자리가 높게 날며 가을을 알리고 있다. 이 때 하늘거리며 푸른 하늘을 나는 잠자리의 날개를 잘 관찰해보자. 잠자리의 날개가 스테인드글라스처럼 되어 있는 것을 발견할 수 있다. 그렇다면 이런 잠자리 날개의 구조를 수학으로도 설명할 수 있을까? 수학은 못하는 것이 없다.

평면을 나누는 수학적 분할 방법에는 무엇이 있을까?

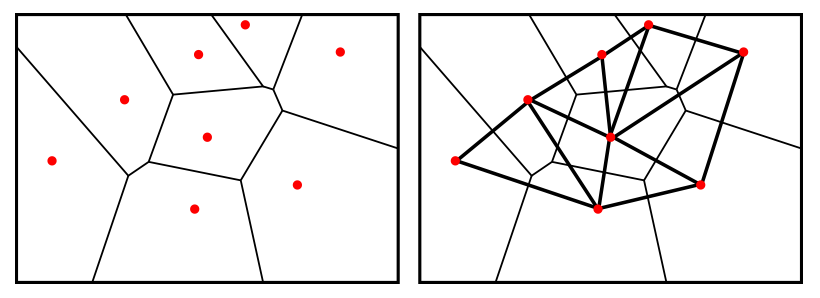▲ 왼쪽부터 보로노이 다이어그램과 델로네 삼각분할을 활용해 평면을 분할한 모습.

수학에는 평면을 나누는 분할 문제가 여러 가지 있다. 그 중에서 평면 위에 주어진 점을 꼭 하나씩만 포함하는 볼록 다각형으로 평면을 나누는 방법이 있는데, 이를 ‘보로노이 다이어그램’이라고 한다. 이것은 20세기 러시아의 수학자 조지 보로노이의 이름을 딴 것이지만, 그보다 훨씬 이전에 수학자이자 철학자였던 그 유명한 데카르트에 의하여 발견된 것으로 추정되고 있다.

한편, 보로노이 다이어그램의 생성점들을 연결하여 삼각형들로 면을 분할하는 방법이 있는데 이를 ‘델로네 삼각분할’이라고 한다. 즉 델로네 삼각분할이란, 평면에 있는 세 점을 잡아 가능하면 정삼각형에 가깝도록 나누는 것이다. 델로네 삼각분할은 이 분야를 많이 연구했던 러시아의 수학자 보리스 델로네의 이름에서 따왔다.

보로노이 다이어그램은 어디서 사용될 수 있을까?

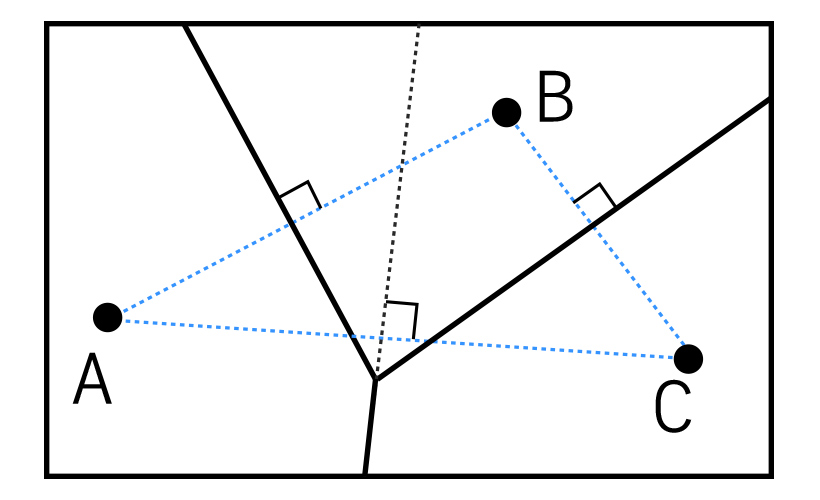▲ 점이 하나씩 포함되도록 평면을 분할한 ‘보로노이 다이어그램’을 나타낸 그림.

보로노이 다이어그램의 가장 중요한 조건은 최대한 가까운 두 점을 수직이등분선을 이용해 점이 꼭 하나씩 포함되도록 평면을 분할해야 한다는 것이다. 즉, 위의 그림에서 AB 두 점을 연결하는 가상의 선분(점선)을 수직 이등분하는 선, 선분 BC를 연결하는 수직이등분선 그리고 선분 AC를 연결하는 수직이등분선을 이용하여 평면을 나눈 것이다.

보로노이 다이어그램은 처음에 소개했던 잠자리의 날개뿐만 아니라 거북이의 등껍질, 기린의 몸에 나타난 무늬 등과 같이 자연에서 그 모습을 쉽게 찾아볼 수 있다. 특히 화산 활동으로 현무암질 용암이 분출되어 냉각되고 수축하며 균열이 생겨서 만들어진 육각형 모양의 주상절리는 대표적인 보로노이 다이어그램 분할 모습이다.

▲ 자연에서 발견할 수 있는 보로노이 다이어그램 분할 모습

보로노이 다이어그램은 의사였던 존 스노우(John Snow)가 1854년 런던에 창궐했던 콜레라의 원인을 추적하는 과정에서 사용했다. 그는 당시 런던에 있던 식수 펌프의 위치를 기준점으로 설정하고 콜레라 발생을 관찰했다. 그 결과 브로드 거리 콜레라 희생자의 대다수가 가장 가까운 식수 펌프의 물을 이용했다는 것을 알아냈다.

여기서 보로노이 다이어그램이 대체 어떻게 쓰였다는 것일까? 약간 이해가 어려울 수도 있겠다. 그렇다면 지금 시국과 맞는 코로나19 상황을 예로 들어보자.

코로나 환자가 어떤 임의의 점이라 하고 나머지 점은 비감염자라고 한다면, 감염자와 가장 가까운 위치에 있는 사람들은 밀접 접촉자가 된다. 따라서 한 점에서 가장 가까운 점으로 전파되고, 다시 그 점에서 2번째 전파가 되는 식이다. 앞서 말한 것처럼, 보로노이 다이어그램에서는 어떤 영역에 꼭 한 점이 포함된다고 했는데, 이 점이 바로 감염자이다. 감염자인 경우, 그 영역에 들어있는 다른 사람은 모두 밀접접촉자로 분류되고 그래서 감염자가 다녀간 식당에 있던 사람은 모두 검사를 받으라고 연락이 오는 것이다.

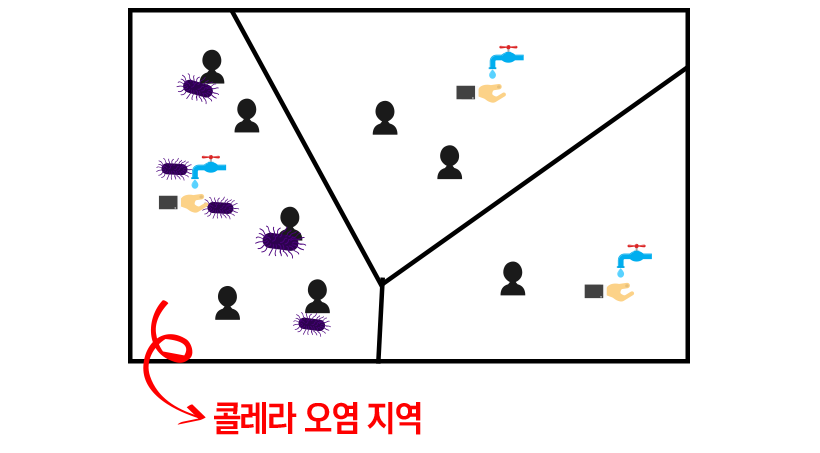
다시 콜레라 발견 사례로 돌아가 보자. 여기서는 점이 식수 펌프가 되는 것이다. 그 영역에 있는 사람들에게 그 우물은 다른 우물보다 접근하기 가장 가깝다. 따라서 그 영역 안에 사는 사람은 모두 그 우물을 이용할 것이다. 만일 그 우물이 오염되었다면 그 영역에 사는 사람은 모두 오염된 물을 먹었을 가능성이 매우 큰 것이다. 이러한 원리를 이용해 존 스노우가 콜레라의 감염 원인을 추적한 것이다.

그는 당국에 식수 문제가 있다고 보고했지만, 이 시기는 세균론이 받아들여지기 전이었으므로 콜레라가 물에 포함된 물질에 의해 발생했다는 주장은 매우 혐오스러운 발상으로 간주했다. 그러나 많은 환자가 같은 식수 펌프를 이용했다는 명확한 증거가 있었기 때문에 보건당국은 펌프의 손잡이를 제거해 펌프를 사용하지 못하도록 했고, 이후 콜레라는 점차 사그라들었다.

한편, 보로노이 다이어그램은 내가 위치한 곳에서 가장 가까운 병원, 약국과 같은 편의 시설을 찾아주는 프로그램에도 활용이 된다. 지리적으로 내가 있는 위치를 기준점으로 하고, 각각의 점들은 생활에 필요한 서비스를 제공해 주는 관청, 편의점, 병원 등의 위치로 생각할 수 있다.

델로네 삼각분할은 어디에 사용할 수 있을까?

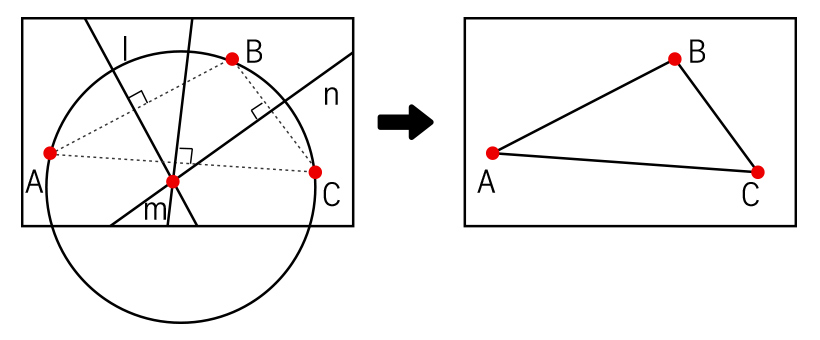▲ 델로네 삼각분할을 나타낸 그림으로, 삼각형 외접원 위에는 딱 세 꼭짓점만 포함한다.

‘델로네 삼각분할’의 가장 중요한 특징은 ‘어떤 삼각형의 외접원도 그 삼각형의 세 꼭짓점을 제외한 다른 어떤 점도 포함하지 않는다.’는 것이다. 따라서 외접원 위에는 딱 세 점만 있게 된다. 삼각형이 홀쭉하고 길수록 외접원도 커지기 때문에 원에 다른 점을 포함할 수도 있다. 그러나 델로네 삼각분할에서는 원에 딱 세 개의 점만 포함된다. 즉, 가능하면 비슷한 거리에 있는 점 3개를 이어서 삼각형을 만들기 때문에 평면이 정삼각형에 가까운 삼각형으로 분할된다.

▲ ‘3D 모델링 구현’과 ‘도로망 설계’에 델로네 삼각분할이 활용된다.

델로네 삼각분할의 가장 중요한 활용 분야는 입체의 표면을 3D 다각형으로 모델링 할 때이다. 물체의 표면에 많은 점을 찍은 후, 이 점들을 기준으로 삼각분할 하면 컴퓨터로 입체의 모양을 가장 그럴듯하게 구현할 수 있다. 즉, 델로네 삼각분할은 정삼각형에 가깝도록 세 점을 잡아 평면을 나눈 것이고, 이러한 원리 때문에 일정한 크기로 면적을 나눌 수 있어 3D 모델링 구현과 같은 곳에 활용되는 것이다.

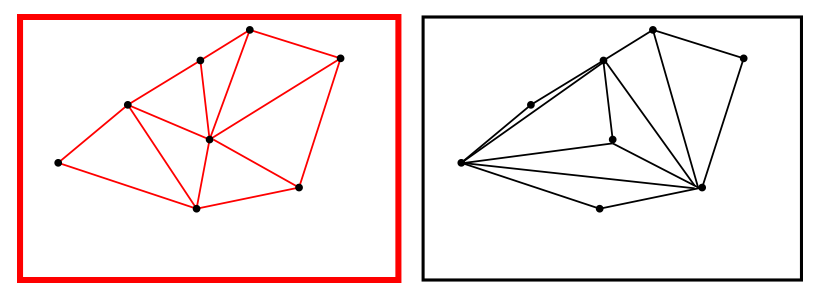▲ ‘왼쪽 그림’은 최대한 가까운 세 점을 잡아 가능한 정삼각형에 가깝도록 삼각형을 분할한 모습으로 델로네 삼각분할을 만족하지만, ‘오른쪽 그림은’ 크기가 일정하지 않은 삼각형이 나오게 꼭짓점을 연결한 그림으로 델로네 삼각분할을 만족하지 않는다.

또, 도시와 도시를 연결하는 도로망을 설계할 때 델로네 삼각분할을 활용하면 우회로 인한 이동 거리의 증가를 최소화할 수 있다고 알려져 있는데, 이게 어떻게 가능한지 살펴보자.

만일 n개의 도시가 있을 때, 모든 도시와 도시를 직접 직선도로로 연결할 경우에는 n개에서 2개를 뽑은 경우의 수와 같으므로 모두 _nC₂=n(n-1)/2개의 도로를 건설해야 한다. 그러나 모든 도시를 서로 직접 연결하는 것은 너무 비효율적이기 때문에 실제로는 일부 도로만을 연결하여 전체 도시들이 연결되도록 한다. 이를테면 도시 A에서 도시 B로 이동할 때, 직접 연결된 도로가 없다면 다른 도시들을 우회해서 이동해야 한다.

이때 중요한 점은 도시 A에서 도시 B로 이동하기 위해 우회한 총 이동거리가 A-B 사이의 직선거리에 비해 최소화되도록 도로망을 설계하는 것인데, 델로네 삼각분할을 이용하여 도로를 연결하면 길고 홀쭉한 삼각형이 나오지 않도록 최대한 가까운 세 점을 잡아 평면을 나누기에 우회에 따른 이동거리의 증가를 최소화할 수 있다.

한편, 델로네 삼각분할은 코로나19의 전파를 추적하는 데도 활용할 수 있다. 최초의 감염자를 찾고 그와 가장 가까운 접촉자를 찾는 방법으로 진행되는 역학조사에서 ‘가장 가까운 접촉자(밀접 접촉자)’를 찾는 방법을 시뮬레이션할 때 활용된다. 이를테면 확진자 P의 밀접 접촉자를 찾을 때, P와 가장 가까운 위치에 있던 사람부터 찾는 방법이 델로네 삼각분할과 같은 원리이다.

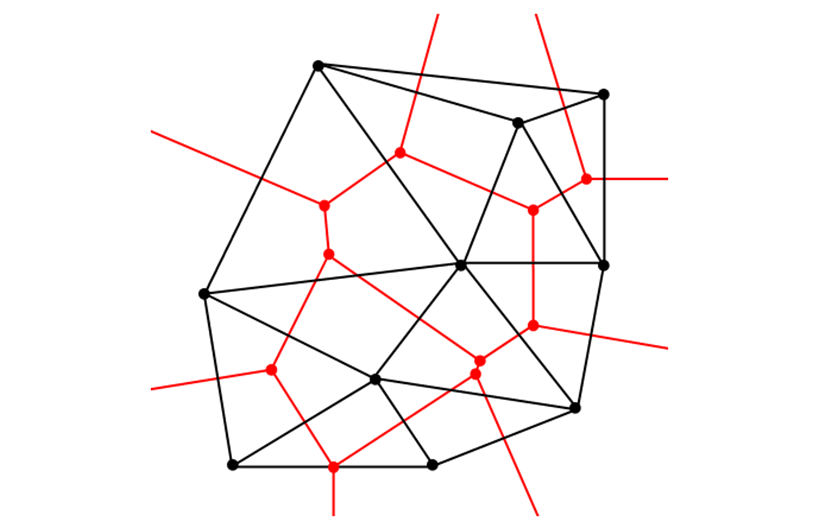▲ 빨간색과 검은색 선은 각각 보로노이 다이어그램과 델로네 삼각분할의 모습을 나타낸다. (출처: 위키피디아)

앞에서 살펴본 ‘보로노이 다이어그램’과 ‘델로네 삼각분할’이 다른 개념을 소개하는 것 같아 보이지만, 두 분할 방법은 어느 하나를 알면 다른 하나도 곧바로 구할 수 있는 ‘쌍대’ 관계에 있다. 즉, 수직이등분선을 이용하여 얻은 분할로부터 삼각형의 외접원을 얻을 수 있으며, 그 외접원 위에 있는 세 점을 꼭짓점으로 하는 삼각형을 얻을 수 있다.

지금까지 단순한 점을 이용하여 평면을 분할하는 방법을 알아보았다. 점처럼 별것 아닌 것으로부터 세상의 다양한 문제를 해결하기 위한 각종 해결책을 발견해 나가는 삶의 해결사가 바로 수학이다. 그러니 수학을 즐길 줄 알면 세상의 많은 문제를 해결할 수 있다. 수학을 어렵게만 생각하지 말고 좀 더 가까이하여 세상의 문제를 해결할 수 있는 시야를 넓히도록 노력해보자.

※ 이 칼럼은 해당 필진의 개인적 소견이며 삼성디스플레이 뉴스룸의 입장이나 전략을 담고 있지 않습니다.