피보나치(Leonardo Fibonacci, 1170년 추정 ~ 1250년 추정)는 잘 알려진 중세 유럽의 가장 뛰어난 수학자이다. 당시 유럽에서는 산술과 표기(로마자)를 다르게 하는 불편함이 있었으나 피보나치가 새로운 인도-아라비아 숫자와 그 수를 이용한 셈법을 유럽에 소개하면서 당시 유럽인들의 불편함을 해소하는 계기를 가져다주었다. 

우리는 그가 저술한 『산반서』라는 책을 통해 이러한 사실을 알 수 있다. 이 책은 1228년에 출판되었다. 모두 15개의 장으로 구성되어 있고 다양한 연산 방법과 사례를 다루고 있다.

피보나치 수열의 역사적 유래

피보나치는 자신의 책에서 처음으로 오늘날 우리가 사용하고 있는 인도-아라비아 숫자와 이 숫자를 사용하여 수를 쓰는 방법과 셈을 하는 방법을 소개했다. 당시 유럽인들은(우리나라를 포함한 동양도 마찬가지로) 계산은 주판으로 하고, 계산 결과를 로마 숫자(동양의 경우는 한자)로 나타내는 번거로운 일을 해야만 했다. 그런데 인도-아라비아 숫자가 도입되며 계산과 표기를 한꺼번에 할 수 있게 되며 수학은 일대 전환기를 맞이한다.

『산반서』에서 새로운 수를 어떻게 활용하는지 알려주려고 제시된 실용적인 문제는 우리에게 중세의 화폐, 무게와 길이, 사업의 실제 계산과 상품 등 다양한 정보를 준다. 더욱이 이 책에 흥미로운 수학 문제가 많이 소개되어 있다. 그런 문제 중에서 특히 우리의 흥미를 끄는 문제는 토끼의 번식에 관한 것이다.

『산반서』의 12장에 있는 수학 문제에 나타난 수열을 1870년대 프랑스의 수학자 루카스(E. Lucas)가 ‘피보나치 수열’이라고 이름 지었는데, 오늘날 이 수열은 자연계뿐만 아니라, 과학, 건축, 예술에 이르기까지 아름답거나 질서정연한 어떤 형식이 있는 곳이면 빠지지 않고 등장하고 있다.

수열과 토끼는 어떤 관련이 있을까?

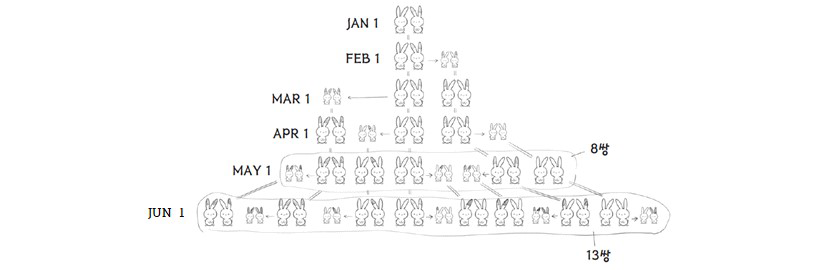▲ 피보나치 수열은 토끼 번식 이야기에서 출발한다.

 “어떤 사람이 토끼 1쌍을 우리에 넣었다. 이 토끼 1쌍은 한 달에 새로운 토끼 1쌍을 낳고, 낳은 토끼들도 1달이 지나면 다시 1쌍의 토끼를 낳는다. 그렇다면 1년이 지나면 몇 쌍의 토끼가 있을까?”

이 문제를 그림을 그려가며 알아보자. 첫 달은 원래 우리에 넣은 토끼 1쌍만이 있다. 두 달째, 처음 토끼 1쌍은 1쌍의 새끼 토끼를 낳을 것이므로 모두 2쌍의 토끼가 우리에 있다. 다음 달, 원래 토끼 1쌍은 또 다른 새끼 토끼 1쌍을 낳고, 처음 태어난 1쌍의 새끼 토끼가 자랄 것이다.

이제 3쌍의 토끼가 우리에 있다. 한 달 후, 처음 토끼 1쌍은 또 다른 새끼 토끼 1쌍을 낳고, 2번째 태어난 1쌍은 자랄 것이다. 그리고 첫 번째 태어나서 다 자란 토끼 1쌍은 다른 새끼 토끼 1쌍을 낳는다. 그러면 우리에는 모두 5쌍의 토끼가 있게 된다. 다섯 번째 달에는 8쌍이 되고 여섯 번째 달에는 13쌍의 토끼가 우리에 있게 된다.

곧 다루기 힘들 정도로 늘어나겠지만, 앞의 그림과 같은 방법으로 계속 그려나갈 수는 있다. 하지만 매달 토끼 쌍의 수를 조사하면 문제를 풀 수 있는 패턴이 아래 표와 같이 나타난다. 이 패턴에서 처음 수로 1을 첨가하면 다음과 같은 규칙과 수열을 구할 수 있다.

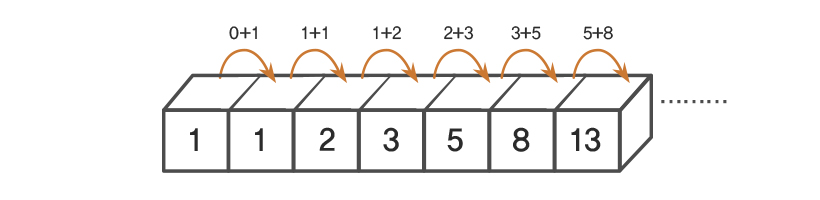
이렇게 해서 나오는 피보나치 수열의 각 항에 있는 수들을 ‘피보나치 수(Fibonacci number)’ 라고 한다. 세계 수학계에서 통용되는 공식적인 피보나치 수열의 일반항에 대한 표현은 피보나치(Fibonacci)의 앞 글자 F를 따서 F_n 으로 나타낸다. 17세기에 대수학의 기호가 발전하면서 수학자들은 이 수열을 공식 F_n+2 =F_n+1 + F_n 으로 만들었다. 즉, _n+2번째 항의 피보나치 수는 _n+1번째와 _n번째 피보나치 수의 합과 같다.

피보나치 수열이 수학적으로 중요한 이유는 여러 가지가 있는데, 그중 하나는 이 수열이 황금비를 만든다는 것이다. 즉, _n+1번째 피보나치 수를  _n번째 피보나치 수로 나누면 그 비율은 점차 1.6으로 수렴한다. 엄밀하게 말하면 수식은 다음 이미지와 같다.

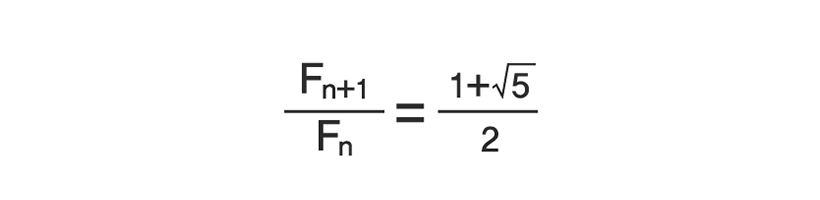
고대 그리스인들은 이 수에 ‘황금비(Golden Ratio)’라는 특별한 이름을 붙였고 기호 Φ (파이)를 사용하는데, 이것은 고대 그리스의 가장 위대한 조각가인 피디아스(Phidias)의 이름에서 따온 것이다.

자연과 디자인에서 찾을 수 있는 피보나치 수열 ‘황금비’

기원전 2000년경의 이집트 아메스(Ahmes)의 파피루스에서는 기원전 4700년에 기자(Gizeh)의 대 피라미드를 건설하는데 황금비를 ‘신성한 비율’로 사용했다고 전하고 있다. 현대의 측량기술은 피라미드의 밑의 중심에서 밑의 모서리까지 그리고 경사면까지 거리의 비가 거의 정확하게 '1: 1.6'이라는 것을 확인시켜주었다.

고대인들은 황금비에서 신비로움을 찾은 것과 동시에 이것으로부터 어떤 안정된 즐거움을 찾았다. 학자들은 고대 그리스로부터 중세에 이르기까지 많은 건축물과 조각상에서 피보나치 수와 황금비를 찾았다. 대표적으로 그리스의 조각가인 피디아스의 조각에서, 파르테논 신전과 다른 그리스 건축물에서 그리고 1180년대에 세워진 크루니 대 수도원에서 찾을 수 있다.

1900년대가 되어 옥스퍼드 대학의 식물학자인 처치(A. H. Church)는 놀라운 발견을 했다. 해바라기꽃의 씨의 형태에서 나선을 이루는 것을 세었더니 그것이 피보나치 수라는 것을 알게 되었다. 처치의 발견 이후로 식물학자들도 자연의 이곳저곳에서 피보나치 수를 찾았다.

예를 들면, 줄기에서 잎의 배아의 배열, 솔방울 비늘의 배열, 데이지의 작은 꽃잎, 솔방울에서 포엽의 배열 등에서 찾을 수 있다.

▲  8:5 (16:10) 황금비를 보여주는 삼성 갤럭시 탭 S6 (출처: 삼성전자)

오늘날의 과학기술에서 피보나치 수열이 나타나는 경우는 너무 많다. 이 수열은 데이터를 분류하고 정보를 검색하는 데에도 이용되고 있다. 최근에는 암호는 물론 컴퓨터과학 분야에서 광범위하게 쓰이고 있다. 특히 약 100년 전, 독일의 심리학자 페흐너(Gustav Fechner)는 수백 명에게 여러 종류의 직사각형을 보여 준 다음, 마음에 드는 것을 선택하게 하는 실험을 했다. 그런데 그 결과 대부분 황금 직사각형을 선택했다고 한다.

가로의 길이와 세로의 길이의 비가 8:5 즉 '8/5 =1.6'인 황금 직사각형은 다양한 제품의 디자인에 활용되고 있으며, 디스플레이 화면에서도 이러한 비율을 찾아볼 수 있다. 예를 들어 갤럭시노트 10.1 2014 에디션과 2019년 8월에 출시된 갤럭시 탭 S6의 화면의 가로와 세로의 비율이' 16:10 =8:5'로 황금 직사각형이다.

이는 제품 디자이너가 소비자에게 더욱 아름다운 영상을 제공하려는 깊은 고민의 결과라고 생각된다. 이처럼 황금 직사각형을 빈번하게 이용하는 이유는 무의식중에도 아름다움을 추구하는 우리의 잠재의식 때문일 것이다. 앞으로도 황금비, 피보나치 수열이 적용된 다양한 제품이 나올 거라 예상해 본다.

※ 이 칼럼은 해당 필진의 개인적 소견이며 삼성디스플레이 뉴스룸의 입장이나 전략을 담고 있지 않습니다.