
전기는 눈에 보이지 않는다. 우리가 보는 것은 ‘전기가 만드는 에너지’이다. TV는 전기를 이용해 빛 에너지와 소리 에너지를 만들고, 선풍기는 전기를 이용해 날개를 돌리는 운동 에너지를 만든다. 이처럼 우리는 전기가 만든 에너지를 보면서 마치 전기를 본 것이라고 착각한다. 그만큼 전기에 대해 정확히 알 필요가 있다. 어렵지만 재미있는 회로 이론에 대해 살펴보도록 하자.
아래 사진은 가장 단순한 전기 회로를 구성한 것이다. 과학을 좋아하지 않는 사람이라도 초등학교 때 한 번쯤은 회로를 꾸며봤을 것이다. 건전지와 전구, 그리고 스위치가 보인다.

위의 회로를 기호로 만든 회로도로 표현하면 훨씬 단순하고 쉽게 그릴 수 있다. 전지에서 긴 막대는 플러스(+) 극을, 짧은 막대는 마이너스(-) 극을 나타내고, 전구와 같은 전기기구들은 모두 저항으로 울퉁불퉁한 선으로 나타낸다.
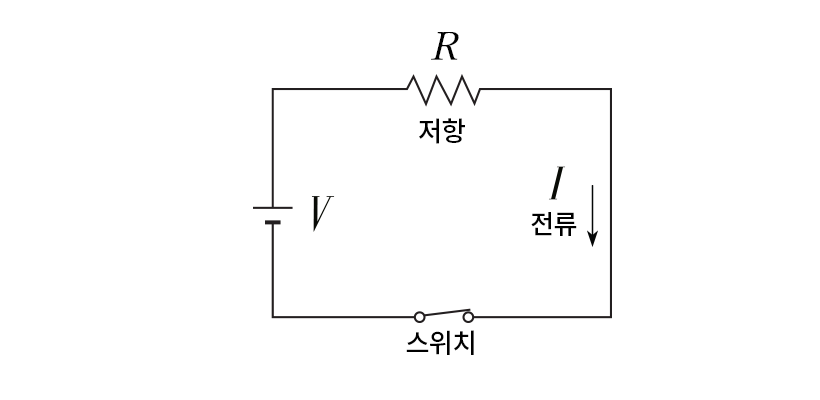
이제 전기 회로를 구성하는 요소들을 하나하나 자세히 들여다보자.
회로를 구성하는 요소들
1. 전위차(Voltage)
여러분이 알고 있는 ‘전압’이란 용어는 사실 공식적인 물리 용어가 아니다. 공식적인 표현은 ‘전위차’이다. 전위차를 알기 위해서는 먼저 전위를 이해해야 한다.
전위는 전기적 위치 에너지를 말하는데, 요즘에는 위치 에너지라는 표현보다 퍼텐셜 에너지를 더 많이 사용한다. 높은 곳에 있는 물체일수록 퍼텐셜 에너지가 커서 더 많은 일을 할 수 있는 것처럼 전기에서도 전위가 높을수록 큰 전기 에너지를 얻을 수 있다.
전지의 플러스(+) 극과 마이너스(-) 극 양 끝의 전위의 차이를 전위차라고 하고 이것을 전기 회로에서 비공식적으로 전압이라고 부른다. 전압의 단위는 이탈리아의 물리학자 ‘알레산드로 볼타(Alessandro Volta)’를 기리기 위해 V를 쓰고, 볼트라고 읽는다.

전압을 쉽게 이해할 수 있는 예가 바로 물레방아이다. 전압이 크면 펌프가 물을 더 높이 퍼 올리게 되고, 높은 곳에서 떨어지는 물은 물레방아를 잘 돌게 할 것이다.
2. 전류(Current)
전기는 눈에 보이지 않으므로 이를 좀 더 쉽게 이해하기 위해 자주 물의 흐름에 비유한다. 물이 높은 곳에서 낮은 곳으로 흐르는 것처럼, 전기 회로에서는 전지의 전위차에 의해 금속에 있는 자유전자들이 이동하게 되는데, 이것을 전류(電流, Electric Current)라고 한다. 전류의 단위는 프랑스 물리학자 ‘앙드레 마리 앙페르’를 기리기 위해 A라고 쓰고, 암페어라고 읽는다.
3. 전기 저항(Resistance)
전기 저항은 전류의 흐름을 방해하는 정도를 의미한다. 전기 저항은 연결된 도선의 길이에 비례하고, 단면적에 반비례한다. 이를테면 도선의 길이가 길고 좁을수록 전류가 통과하기 어려우므로 저항이 크다. 예를 들면 지하철 개찰구를 여러 사람이 한꺼번에 통과하려면 힘든 것과 같이 말이다.

요즘은 보기 힘들지만 예전에 화장실 전등으로 많이 썼던 백열전구는 매우 가느다란 텅스텐 합금을 길게 뽑아내 만든 필라멘트의 전기 저항을 이용했었다.
4. 소비 전력(Electric Power)
저항에 전류가 흐르게 되면 저항에서는 전기 에너지를 소비한다. 전기를 이용해 작동하는 기기나 장치들은 모두 저항이라고 생각해도 좋다. 기기마다 전기 에너지를 소비하는 형태가 달라서 전기다리미의 경우에는 전기 에너지를 열에너지로, 전구는 전기 에너지를 빛 에너지로 소비한다.
저항에서 1초 동안 소비하는 전기 에너지를 소비 전력이라고 한다. 소비 전력의 단위는 W라고 쓰고, 와트라고 읽는다. 가정에서 사용하는 전구에는 소비 전력이 표시되어 있는데, 100W인 전구가 60W인 전구보다 밝은 이유가 1초 동안 소비하는 전기 에너지가 100W인 전구가 더 크기 때문이다.
내 몸 속의 체지방, 옴의 법칙으로 정복한다.
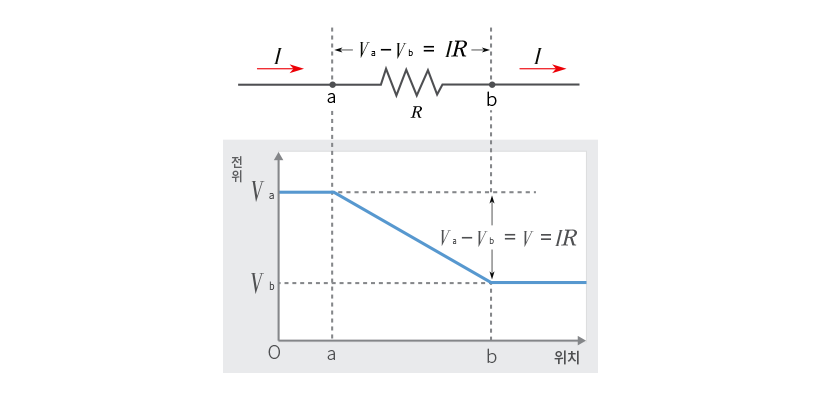
그림과 같이 전기 저항의 양쪽에 전위차가 생기면 전위가 높은 곳에서 낮은 쪽으로 전류가 흐르고 저항에서는 전기 에너지를 소비한다.
이때 흐르는 전류의 세기는 전위차에 비례한다. 같은 양이더라도 수도꼭지에서 흘러나오는 물의 세기보다 폭포에서 떨어지는 물의 세기가 더 큰 것과 같은 이치이다. 또 흐르는 전류의 세기는 전기 저항에 반비례한다. 저항이 클수록 전기의 흐름을 방해하는 정도가 더 크기 때문이다.
이와 같이 전류의 세기(I)와 전위차(V), 전기 저항(R)의 관계를 정리한 사람이 독일의 물리학자 게오르크 시몬 옴(Georg Simon Ohm)이고, 이것을 ‘옴의 법칙(V=IR)’이라고 한다.
 ▲ 옴의 법칙을 활용한 ‘체성분 분석 기계’
▲ 옴의 법칙을 활용한 ‘체성분 분석 기계’
이러한 옴의 법칙은 우리 몸에 있는 체성분을 측정하는데 활용된다. 우리 몸에 있는 지방은 수분이 적게 포함되어 있고 근육은 수분 함량이 높다. 물은 전기를 잘 통하게 하는 성질이 있는데 이를 이용하면 우리 몸에 근육이 얼마나 있는지, 지방이 얼마나 있는지 예상하는 것이다.
복잡한 회로야 가라, 키르히호프의 법칙
키르히호프는 전자기 분야에서 많은 연구 결과를 남겼을 뿐만 아니라 분광학(물질이 흡수하거나 방출하는 빛의 스펙트럼을 분석하는 학문)에서도 뛰어난 업적을 남긴 독일의 물리학자이다. 전기 회로 중 복잡한 회로에서 각 도선에 흐르는 전류의 세기와 방향을 구할 때 키르히호프의 법칙을 사용하면 보다 간편하게 구할 수 있다.
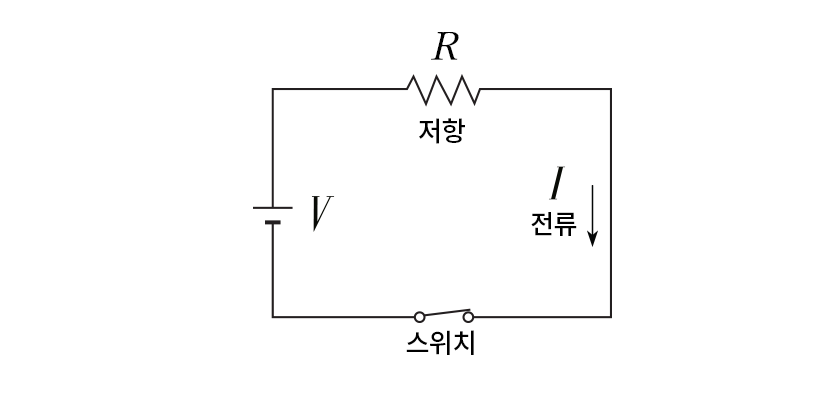
위 그림과 같이 단순한 전기 회로의 경우 옴의 법칙을 써서 전지에서의 전위차를 V, 전기 저항을 R, 회로에 흐르는 전류의 세기를 I라고 한다면 전류의 세기는 'I=V/R'로 간단하게 구할 수 있다.
하지만 다음의 회로를 보자. 전지가 서로 다른 도선에 3개나 있어서 각각의 도선에 흐르는 전류의 세기를 구하기가 쉽지 않다. 이런 경우 키르히호프의 법칙을 이용하면 보다 손쉽게 우리가 원하는 값들을 구할 수 있다.
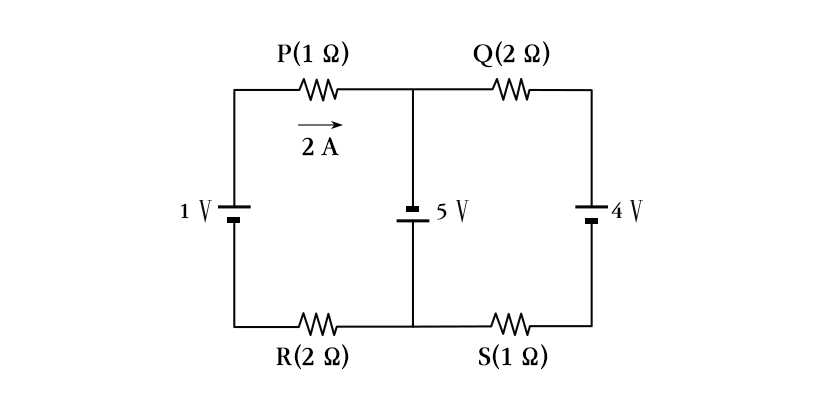
키르히호프의 법칙은 크게 두 가지로 구성되어 있는데, 1법칙은 전하량 보존 법칙으로 도선이 갈라지거나 합쳐질 때 전류값이 보존된다는 것이다. 2법칙은 에너지 보존 법칙으로 루프(loop) 회로에서 전지가 만든 전위차는 저항에서 감소한 전위차와 같다는 것이다.
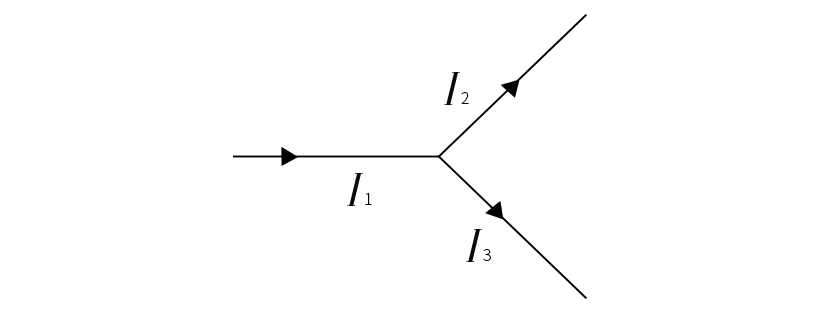
위의 이미지는 1법칙을 그림으로 표현한 것으로 도선이 갈라지기 전의 전류의 세기I1과 갈라진 후의 전류의 세기 I2·I3 의 합은 같다는 것이다. [전하량 보존법칙]
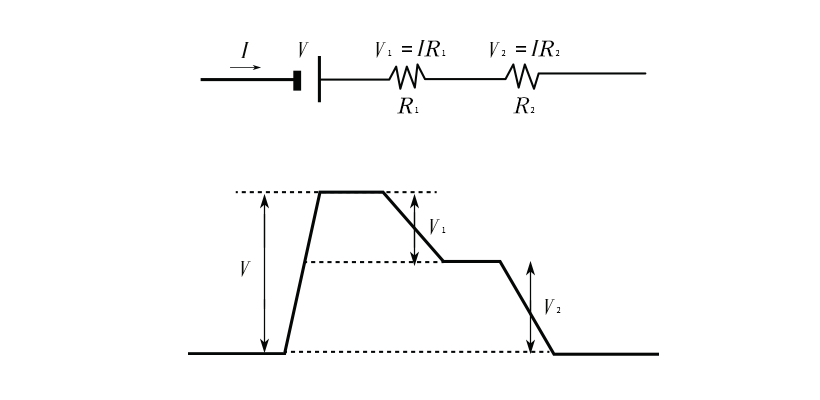
위 이미지는 2법칙을 표현한 것으로 전지에서 만든 전위차 V는 각 저항에서 감소한 전위차 V1· V2의 합과 같다는 것이다. [에너지 보존 법칙]
 ▲ 키르히호프 법칙을 활용한 ‘차량 배터리 점프’
▲ 키르히호프 법칙을 활용한 ‘차량 배터리 점프’
자동차가 시동이 안 걸리면 다른 차의 배터리와 연결해 시동을 거는 방법이 있는데 보통 ‘점프’한다고 한다. 점퍼선은 회로에서의 도선이 되며 각각의 자동차의 배터리는 전지 역할을 한다. 이때 회로에 흐르는 전류, 충전하여 얻는 전위차 등을 구할 때에도 키르히호프의 법칙을 이용한다.
지금까지 전기회로와 관련된 기초적인 정의와 이론들을 알아보았다. 우리가 일상에서 널리 사용하는 전기는 눈에 보이지 않지만 수많은 원리와 법칙들이 담겨 있다. 이러한 지식들을 알고 있다면 일상에서 전기를 보다 효율적이고, 안전하게 사용할 수 있을 것이다.
※ 이 칼럼은 해당 필진의 개인적 소견이며 삼성디스플레이 뉴스룸의 입장이나 전략을 담고 있지 않습니다.

