
자연의 움직임은 어떠한 차이로 인해 불균형이 생길 때 발생합니다. 기압 차이로 인해 바람이 불고, 온도 차이로 인해 열이 전달되며, 전압 차이로 전류가 흐릅니다.
여기서 바람의 흐름(기류), 열의 흐름(열류), 전기의 흐름(전류) 등을 총칭하여 플럭스(flux)라 합니다. 쉽게 말하면 무엇이든 흘러가는 것을 말합니다. 또 이런 흐름을 만들어내는 전압, 압력, 온도와 같은 구동력을 퍼텐셜(potential)이라 합니다.
퍼텐셜과 플럭스는 이런 자연 흐름뿐 아니라 사회 문화 현상에도 적용이 가능합니다. 백범 김구 선생이 꿈꾸었던 '진보된 문화'라는 것도 일종의 퍼텐셜이고, 문화 차이에 의해 발생하는 한류와 같은 흐름을 플럭스가 발생했다고 할 수 있습니다. 오늘은 이런 퍼텐셜과 플럭스에 대해 알아보겠습니다.
퍼텐셜(potential)은 뭘까?

초등학교 때 플라스틱 책받침 위에 쇳가루를 올려놓고 아래에 자석을 갖다 대는 실험을 한 적이 있을 것입니다. 자석 주위로 자기장이 형성되고 N극에서 나와 S극으로 향하는 자력선이 만들어집니다. 자기장과 같이 공간내 위치에 따라 함수값이 변화하는 공간을 장(場)이라 합니다.
우리가 잘 알고 있는 장으로는 자기장을 비롯해서 중력장, 전기장, 압력장, 온도장 등 많이 있습니다. 장을 이루고 있는 중력, 압력, 온도, 전압 등과 같은 퍼텐셜(F)은 흐름을 만드는 구동 에너지로서 공간상에서 위치에 따라 다른 값을 가집니다. 즉 퍼텐셜은 물리학에서는 장을 기술하는 중요한 개념이며, 수학적으로는 공간좌표에 대한 함수로서 F=F(x,y)와 같이 나타낼 수 있습니다.

중력장의 경우 퍼텐셜은 위치에너지에 해당하며, 수직 높이에 의해서 결정됩니다.
즉, 어느 경로를 통해 그 지점에 도달하건 상관없이 지점 고유의 퍼텐셜 값(중력장의 경우 위치에너지)을 가지게 됩니다. 여기서 퍼텐셜 값이 일정한 점(F=const)들을 이은 선을 등퍼텐셜 라인(iso-potential line) 이라고 합니다.
예를 들어, 고도가 같은 지점을 연결한 선을 지도에서 등고선이라 하고, 온도가 같은 지점을 연결한 선을 등온선이라 합니다.
기울기를 나타내는 벡터량, 그래디언트(gradient vector)
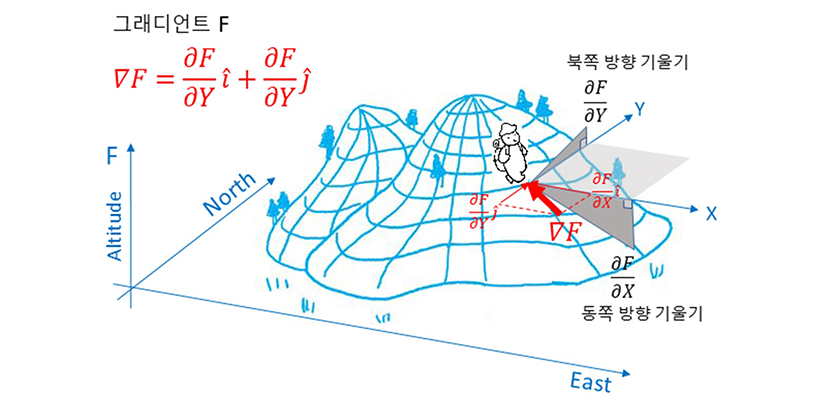
플럭스는 무엇인가 흘러가는 것이라고 했던 것 기억 나시죠? 높은 곳에서 낮은 곳으로 물이 흐르듯이, 플럭스는 퍼텐셜의 기울기에 비례합니다. 산의 기울기를 예로 들면, 산 높이 함수(F: 고도)를 미분한 것이 기울기인데 이것은 하나가 아닙니다. 동쪽 방향(x)으로 기울기와 북쪽 방향(y)으로 기울기가 각각 따로 존재하고 크기도 서로 다릅니다. 기울기를 나타낼 때, 변수가 여러 개 있으면 함수의 기울기도 여러 개가 됩니다.

실제로 산비탈에 섰을 때, 산 기울기는 방향에 따라서 달라지는 것을 경험합니다.
한쪽 방향으로 가파르더라도 다른 쪽 방향으로는 완만합니다. 그렇기 때문에 산의 기울기는 x, y방향으로의 기울기를 나타내는 벡터량으로 이해할 수 있습니다. 이것을 '기울기 벡터' 또는 '그래디언트(gradient vector)'라고 합니다.
지도에 나타난 등고선의 예를 들면, 그래디언트 벡터의 방향은 등고선을 직각 방향으로 끊는, 즉 기울기가 가장 급한 방향을 가리키며, 그래디언트 벡터의 크기는 가장 기울기가 급한 방향의 기울기 값을 가집니다. 등고선 간격이 촘촘할수록 경사가 급한 지역이고 간격이 넓을수록 기울기가 완만한 지역을 의미합니다.
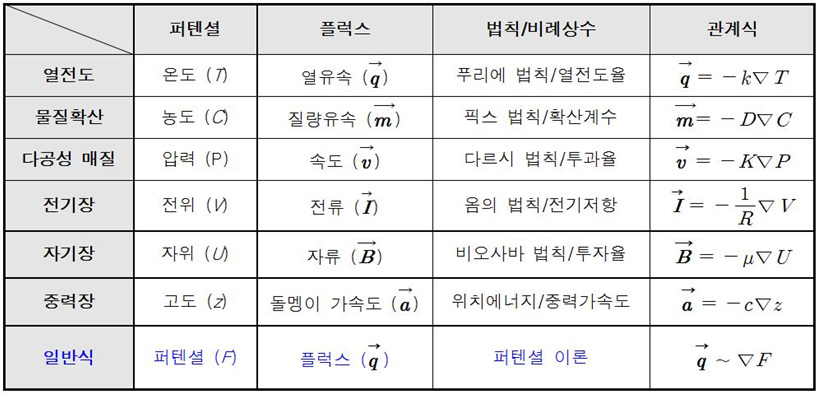
▲ 퍼텐셜과 플럭스의 관계
자연 현상에서 대부분의 흐름은 퍼텐셜의 그래디언트에 비례해서 일어납니다. 열전달량은 온도 기울기, 즉 온도 그래디언트에 비례합니다. 이것을 푸리에 법칙(Fourier’s law)이라 하며, 이때 비례상수를 열전도율이라 합니다. 열과 마찬가지로 오염물질은 농도 그래디언트에 비례해서 확산됩니다. 전류 역시 전압 그래디언트에 비례하는데 이를 옴의 법칙(Ohm’s law)이라 합니다. 위 도표는 퍼텐셜 그래디언트에 비례하는 여러 가지 플럭스의 예를 보입니다.
퍼텐셜 이론
앞서 설명한 자석 주위의 자장에서 쇳가루는 특정한 방향으로 나열되는데 이 방향이 바로 자력선 방향(검은색 점선, 자기플럭스 방향)입니다. 자력선의 직각 방향으로 자위가 일정한 등자위선(컬러 실선, 자기퍼텐셜이 일정한 선)이 형성됩니다. 전체 공간은 등자위선과 자력선이 서로 직교하는 격자 형태를 이룹니다.
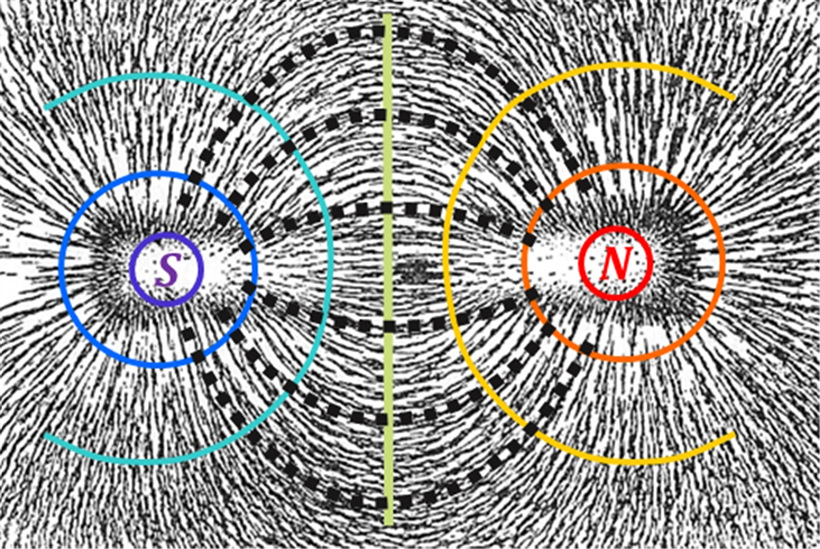 ▲ 자석 위에 형성된 자력선의 모습 (출처: 공대생도 잘모르는 재미있는 공학이야기)
▲ 자석 위에 형성된 자력선의 모습 (출처: 공대생도 잘모르는 재미있는 공학이야기)
위 그림에 나타난 N극과 S극 대신 전기적 양극과 음극으로 대치하면 자기장 대신 똑같은 모양의 전기장 분포가 됩니다. 이때 점선은 전류가 흐르는 전류선이 되고 실선은 전압이 일정한 등전위선이 됩니다. 이번에는 N극과 S극을 대신하여 고온의 물체와 저온의 물체로 대체하면 점선과 실선은 각각 고온에서 저온으로 흐르는 열류선과 온도가 일정한 등온선이 됩니다. 또 N극을 산봉우리, S극을 분지로 생각하면 실선은 등고선이 되고, 점선은, 관성력을 무시할 수 있다면, 돌멩이나 물이 흐르는 방향이 됩니다.
퍼텐셜 이론은 퍼텐셜과 플럭스의 관계를 하나의 법칙으로 설명합니다. 즉 전기장, 자기장, 중력장 등은 모두 앞에서 설명한 그래디언트 법칙을 만족시키고 동시에 보존법칙을 만족시켜야 하므로 이들은 두 법칙을 조합한 라플라스 방정식의 해가 됩니다. 따라서 이들 분포는 물리 현상이 다르더라도 결과적으로 동일한 분포를 보입니다.

서로 직교하면서 격자망을 형성하는 퍼텐셜-플럭스의 짝(pair)을 쉽게 이해하려면, 3차원 입체 형상으로 시각화하면 좋습니다.
퍼텐셜이 높은 쪽은 위로 솟아 있고 낮은 쪽은 아래로 내려가 있는 입체를 머릿속에 그려 봅니다. 이때 플럭스는 등퍼텐셜 라인을 수직으로 끊으면서 그래디언트 방향으로 흘러갑니다. 일상 속에서는 이를 활용한 사례들이 많은데, 그 중 하나가 3D 프린터 기기와 3D 지형도 조작기입니다. 우리는 퍼텐셜 그래디언트와 플럭스의 관계를 통해서 세상의 여러 가지 움직임을 이해할 수 있을 것입니다.

