
2차 세계대전이 발발하기 몇 년 전인 1927년 제 5차 솔베이 회의에는 많은 물리학자가 참석했다. 참석한 물리학자 29명 중 무려 18명이 노벨상 수상자다. 양자역학의 큰 획을 그었던 솔베이 회의를 역사가들은 이렇게 얘기한다. "과학사에서 그렇게 짧은 시간에, 그렇게 소수의 사람들에 의해, 그렇게 많은 것이 밝혀진 적은 없었다"라고. 아인슈타인과 보어 사이에 오간 유명한 담론인 "신은 주사위 놀이를 하지 않는다(아인슈타인)", "신이 주사위 놀이를 하든 말든 당신이 상관할 바 아니다(보어)"도 이 회의에서 나온 얘기다.
 ▲ 보어와 아인슈타인의 담론 장면 (출처: 위키백과)
▲ 보어와 아인슈타인의 담론 장면 (출처: 위키백과)
두 사람 사이의 담론에서 아인슈타인의 말은 양자론의 불완전성을 비꼬는 말이다. 양자론은 자연현상을 일정한 수준에서는 바르게 표현하고 있지만, 완전하지 않기 때문에 확률이라는 생각으로 시작할 수밖에 없다. 즉 자연현상은 어떠한 물리량으로 결정되어 있다는 아인슈타인의 생각과 상반되는 양자론은 그의 입맛에 맞을 수 없었다.
하이젠베르크의 불확정성의 원리
 ▲ 하이젠베르크 불확정성원리에 관한 기념우표 (출처: Amazon)
▲ 하이젠베르크 불확정성원리에 관한 기념우표 (출처: Amazon)
하이젠베르크는 1901년 독일 뷔르츠부르크에서 태어났다. 그의 나이 24세에 라이프치히 대학교에서 교수직을 제안했지만, 제안을 거절하고 양자역학 해석 문제를 연구하기 위해 덴마크 코펜하겐에 있는 보어를 찾아가 비정규직 연구원을 자청한다. 그리고 이를 통해 노벨 물리학상을 받게 된다. 하이젠베르크는 오직 측정 가능한 것만 이론으로 삼는다는 실증주의 신념을 과감히 깨뜨린다. 위치와 운동량을 동시에, 정확하게 측정하는 것은 절대 불가능하다는 것이 그의 핵심적 주장이었다.

우리에게 친숙한 거시세계에서 움직이는 물체의 운동량은 속도와 이동한 거리를 가지고 정확히 측정할 수 있다. 대포를 이용해 10kg의 포탄을 초속 300미터의 속도로 발사되도록 한다면, 몇 분 후 어디에 떨어지는지 알 수 있다. 고전물리학의 기본 전제인 결정론적 미래 예측이 가능한 예다.
하지만 미시세계에서는 이러한 법칙이 통하지 않는다. 전자가 너무 작기 때문에 우리가 빛을 이용해 전자의 위치와 운동량을 관찰하려고 하면, 빛(광자)에 영향을 받아 측정이 부정확해 지는 것이다. 따라서 미시세계에서의 포탄은 관찰하려는 순간 그 위치가 결정된다. 그 전까지는 어디에 떨어질지 확률만 알 수 있을 뿐이다.

쉽게 표현하자면, 전자의 운동량을 측정하는 순간 위치는 계속 변하기 때문에 위치를 정확히 측정하지 못하고, 시작점과 도착점 사이 어디쯤에 있을 것이라고 할 수 있다. 반대로 사진 찍듯이 움직이는 물체를 찍으면 위치는 정확하게 측정된다. 그러나 선명한 사진만 보고서 그 물체가 얼마의 속도로 움직이는 지는 동시에 알아내지 못한다. 사진 상으로는 정지된 것처럼 보이기 때문이다. 이는 측정 수단이 주는 불확정성을 뜻한다.

물의 온도를 측정하려고 하는데, 온도계 자체의 열이 있기에 물의 온도를 약간이라고 변하게 만든다는 말이 있다. 즉, 관찰 수단 자체가 지닌 물리적 특성으로 인해, 관찰 대상의 실제 값이 왜곡되어 정확한 정보를 추출할 수 없다는 것이다. 관찰자의 관찰 행동 자체가 전자에 영향을 주기 때문에 어떠한 관찰수단을 썼느냐에 따라 그 값은 불확실 정도가 달라진다는 것이다. 이를 하이젠베르크의 불확정성의 원리라고 한다.
불확정성(상보성)의 원리와 전자 구름 해석
양자역학에서 상보성의 원리(complementarity principle)는 광자 또는 전자가 파동의 특성을 보이기도 하고 입자의 특성을 보이기도 한다는 원리다. 이는 보어가 코펜하겐 연구소에서 불확정성 원리를 해명하기 위해 도입했다. 달리 말하자면, 물질을 이루는 기본입자들은 입자로 취급할 수도 파동으로 취급할 수도 있지만, 입자와 파동을 동시에 볼 수는 없다는 것이다.
파동론에 의하면 파장을 알고 있기에 운동량(p=h/l)을 명확히 알고 있지만, 입자론에 의하면 위치량(q)은 확실하되 그 이후의 행방은 모른다. 빛의 이중성에서와 같이 관찰하기 전에는 p, q 성질이 공존하지만 관찰하는 순간, p 관찰시 q가 소멸되고 q 관찰시 p가 소멸된다.
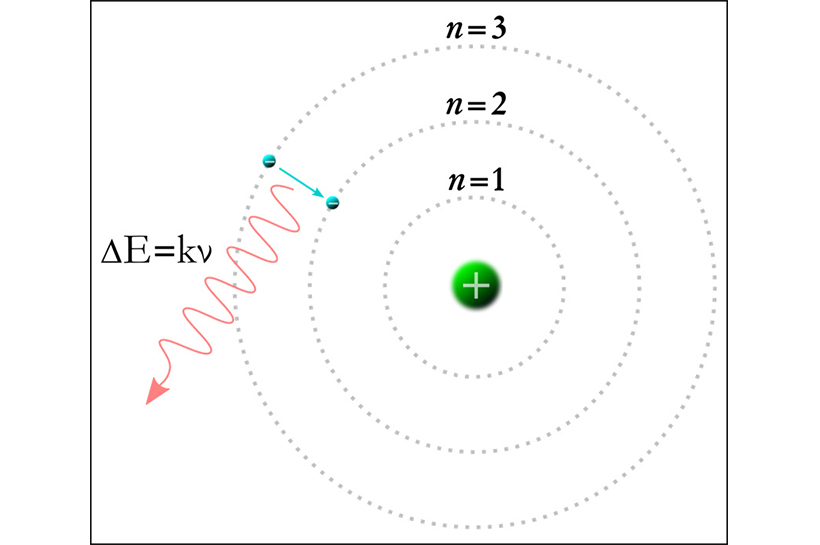 ▲ 원자내 전자궤도 (출처: 위키백과)
▲ 원자내 전자궤도 (출처: 위키백과)
전자가 보어의 원자 모델에서 임의의 운동량을 지니면서 n 궤도를 돌고 있다고 하면, 위치는 n 궤도이고 운동량은 전자의 운동속도로 모든 정보를 동시에 보이게 된다. 그렇지만 전자가 궤도를 옮길 때 전자의 위치량 정보가 사라지듯, 운동하는 양자가 특정 위치에 귀속되는 것은 불확정성 원리에 맞지 않는다. 따라서 원자 내에 귀속되는 전자는 분명 원자 내부 어느 공간 영역에 분포하여 존재해야 할 것이다.
전자를 원자 내부에 가둘 수 있는지는 ΔpΔq=h(불확정성 원리의 수식)를 활용해 계산할 수있다. 결론적으로 원자의 크기에 2만 배나 작은 공간(핵)에 전자를 가두기 위해서는 3.77 eV가 필요하다. 따라서 전자는 핵에 갇혀 있지 않고 원자 내부 어딘가에 존재하게 된다.
따라서 원자가 지닌 에너지가 미치는 범위내에서 전자가 존재해야 하며, 그 범위 내에서만 운동량을 지닌 채 분포하게 된다. 이로써 보어의 궤도 모델은 전면 부정되며, 불확정성의 원리에 의해 특정 위치가 아닌 존재 확률분포 형태로 전자들이 퍼져 있게 된다. 전자의 운동량을 명확히 알면 위치량의 불확정성이 높아지기 때문에 원자 내부라는 제한된 공간 내에서 전자는 정확한 지점이 아닌, 확률분포 즉, 전자구름(electron cloud) 형태로 나타나게 된다.
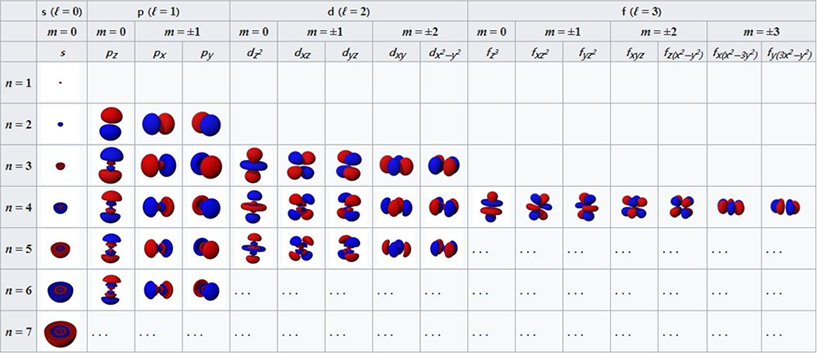 ▲ 오비탈에 따른 전자 확률 분포 (오비탈 : 전자가 나타날 위치를 무수히 많이 겹쳐 표현하면 나타나는 모습 / 출처: 위키백과)
▲ 오비탈에 따른 전자 확률 분포 (오비탈 : 전자가 나타날 위치를 무수히 많이 겹쳐 표현하면 나타나는 모습 / 출처: 위키백과)
존재 확률에 관한 확률밀도로 나타낸 전자구름 모델에서, 전자가 해당 구름 내에 동시에 모든 위치에 있다는 뜻은 아니다. 구름의 밀도가 높은 곳은 수백 번 측정 시 해당 위치에서 발견될 확률이 높다는 것을 나타낼 뿐이다. 확률상 존재할 수 있는 위치를 나타낼 뿐 정확한 위치량은 아니다. 전자의 위치를 관찰하는 순간, 전자구름속에 존재하던 전자는 한 점을 중심으로 수축하고, 다시 관찰행위를 그만두면, 전자는 또다시 전자구름 형태로 존재하게 된다.
앞에서 말했듯 양자의 세계에서 입자의 위치와 운동량 모두를 정확하게 측정하기란 불가능하다. 확실한 것만 다루는 것으로 알려진 물리학에서 ‘나도 모르겠다’라고 외치는 것과 같은 불확정성의 원리는 세상 모든 것이 확실한 물리학의 기반으로만 구성된 것은 아니라는 것을 일깨워 준다.

