자연 현상이나 공학 문제를 수학식으로 표현한 것을 수식화 또는 공식화(formulation)라고 한다면, 이를 행하기 전에 수행하는 것을 차원해석(dimensional analysis)이라고 합니다. 차원해석이란, 관련 물리 변수들을 도출하고 이들을 구성하는 기본차원을 살펴봄으로써 변수들의 관계를 개략적으로 파악하는 수학적 방법을 말합니다.

 *기본차원이란, 모든 유도차원을 만들 수 있는 길이(L), 시간(T), 질량(M) 등 7개의 독립적인 차원을 말한다.

수식의 동차성

수식에 나타나는 변수들은 각기 차원(단위)을 가지고 있으며, 이들의 조합으로 이루어진 항들 역시 특정한 차원을 가지게 됩니다. 수식에는 등호를 중심으로 좌변과 우변이 있고, 각 변은 하나 또는 여러 개의 항으로 이루어집니다. 항이란, 물리 변수들의 조합으로 이루어진 변수 덩어리로서 덧셈이나 뺄셈 기호로 연결됩니다. 여기서 중요한 것은 수식을 이루는 각항들은 모두 같은 차원과 같은 단위를 가져야 한다는 점입니다. 이를 차원의 동차성(dimensional homogeneity)이라 합니다.

▲ 서로 다른 차원(단위)의 물량은 더하거나 뺄 수 없다.

 예를 들어 면적과 길이, 질량과 열량, 그리고 키와 몸무게처럼 차원이 다른 물리량을 서로 더하거나 뺄 수 없습니다. 영어 표현에 ‘오렌지와 사과’라는 말이 있습니다. 같은 기준으로 비교 평가할 수 없는 것을 동일 선상에 올려놓으려 할 때 쓰는 표현입니다.

버킹엄의 파이 정리

차원해석을 정리하기 위해서는 ‘Buckingham의 Pi 정리’를 알아 둘 필요가 있습니다. 버킹엄의 파이 정리는 물리 현상을 지배하는 관련 변수가 모두 k개이고 이들을 이루는 기본차원이 r개라면, 무차원 변수는 k-r개 유도될 수 있다는 사실을 설명합니다.

일반적인 변수를 나타내는데 엑스(X)를 쓰는 것처럼 파이(Π)는 무차원 변수를 나타내는 그리스 문자입니다. k개의 변수들 사이의 관계가 X₁ = f(X₂, X₃, ... , X_k) 와 같이 주어질 때, 각 변수의 거듭제곱(X₁X₂^aX₃^bX₄^c....)으로 이루어진 무차원변수를 k-r개 구할 수 있고, 이들 사이의 관계를 Π₁ = F(Π₂, Π₃, ... , Π_k-r)와 같이 표현할 수 있습니다. 즉, 차원해석을 수행함으로써 변수를 줄여 문제를 단순화하고 변수들 사이의 관계를 쉽게 분석할 수 있다는 뜻입니다.

코코넛 낙하속도

예를 들어 나무에 매달린 코코넛 열매가 땅으로 떨어질 때의 낙하속도를 구해보고자 합니다. 우선 낙하속도 v를 결정하는 변수로, 코코넛 질량 m, 매달린 높이 h, 그리고 중력가속도 g를 들 수 있습니다. 즉 v=f(m,h,g) 입니다. 각 변수를 기본차원으로 표현하면 [v]=[L/T], [m]=[M], [h]=[L], [g]=[L/T²]입니다. 여기서 대괄호는 변수의 값이 아닌 차원을 나타냅니다. 변수의 개수가 총 4개이고, 사용된 기본차원이 M, L, T, 3개이므로 버킹엄의 파이정리에 따라서 4-3=1개의 무차원 변수가 나옵니다. 이어서 각 변수에 대한 거듭제곱의 곱, v¹m^ah^bg^c 이 무차원이 되도록 하는 a, b, c를 구하면 0, -1/2, -1/2가 됩니다. 따라서 무차원변수는 다음과 같이 됩니다.

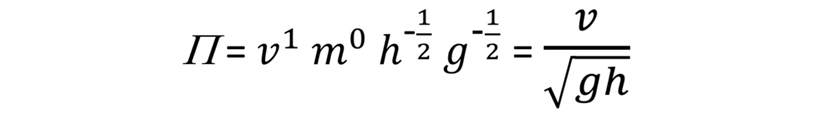
이것은 이 문제에서 나올 수 있는 유일한 무차원변수이므로, Π=F(.) 라 쓸 수 있습니다.

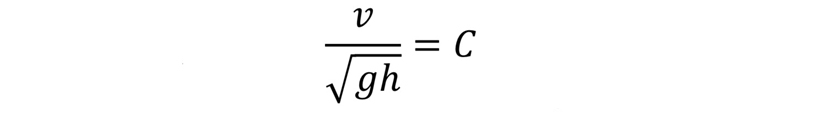
이 식으로부터 낙하속도 v를 구하면 나무 높이 h의 제곱근에 비례한다는 사실과 질량 m에 무관하다는 물리적 사실을 알 수 있습니다. 비록 상수 값 C를 구하지는 못하지만, 물리법칙을 전혀 적용하지 않은 상태에서 단순히 차원만을 분석함으로써 여러 가지 중요한 물리 현상을 끄집어낼 수 있습니다.

칠면조 조리

만약 여러분들이 슈퍼에서 3.5킬로그램짜리 칠면조를 사왔다고 가정해봅니다. 칠면조의 무게는 3.5kg이지만 겉표지에 적힌 조리방법은 7kg을 기준으로 했을 때 6시간 동안 오븐에 두라고 설명되어 있었습니다. 그렇다면 여러분들은 크기가 절반인 칠면조를 익히기 위해 6시간의 절반 시간인 3시간을 두어야 할지, 아니면 똑같이 6시간을 두어야 할지가 고민하게 될 것입니다.

우선 조리시간 t는 칠면조의 질량 m, 그리고 살코기의 밀도 ρ와 열확산계수 α에 의해서 결정된다는 것을 가정합니다. 즉, 익는다는 것은 열이 표면으로부터 내부로 확산되어 칠면조 중심까지 일정 온도에 도달하는 과정이라고 생각한 것입니다. 여기서 각 변수의 거듭제곱이 무차원이 되도록 하면 Π = t¹m^-2/3ρ^2/3α¹ 가 구해집니다. 이 문제에서도 무차원변수가 한 개이므로 상수가 되어야 합니다.

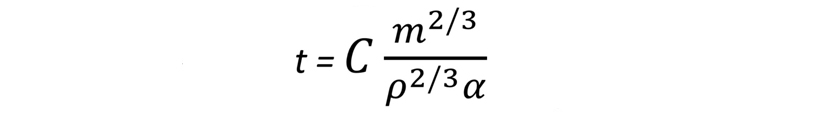
칠면조가 크건 작건 밀도 ρ나 열확산계수 α등 살코기 물성치는 일정하다고 가정할 수 있으므로, 조리시간 t는 칠면조 질량 m의 2/3제곱(또는 길이 L의 제곱)에 비례한다는 것을 알 수 있습니다. 따라서 질량이 절반이면 6시간의 0.5^2/3(=0.63)배이어야 하므로 3시간 47분이라는 결과가 나옵니다.

▲ 칠면조 조리시간에 대한 차원해석 (출처: 공대생도 잘 모르는 공학이야기)

피타고라스 정리

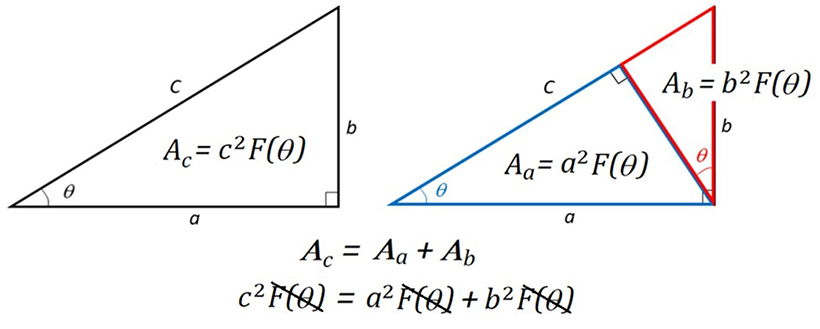▲ 차원해석을 통한 피타고라스 정리의 증명

차원해석을 활용하면 피타고라스 정리도 쉽게 증명할 수 있습니다. 직각삼각형의 면적 A_c를 구하는 공식을 몰라도, 빗변의 길이 c와 한쪽의 각도(라디안) θ를 알면 면적을 구할 수 있습니다. 즉, A_c = f(c, θ) 라고 쓸 수 있고, 차원해석을 하면 아래와 같이 두 개의 무차원변수가 나옵니다. 즉 Π₁ = F(Π₂)입니다. 두 무차원 변수 중 하나가 결정되면 다른 하나가 결정된다는 것을 말합니다.  

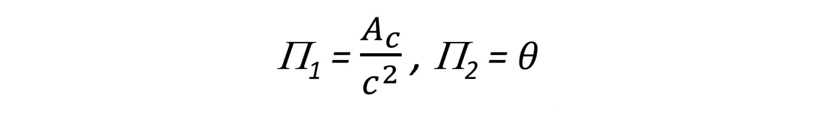
삼각형의 직각 꼭지점에서 빗변으로 수직선을 내리면 하나는 a를 빗변으로 하고, 다른 하나는 b를 빗변으로 하는 닮은꼴 직각삼각형이 됩니다. 두 개의 작은 삼각형에 대해서도 무차원변수 사이의 관계를 똑같이 쓸 수 있습니다. 그런데 두 삼각형 면적의 합은 큰 삼각형의 면적과 같으므로 a²F(θ) + b²F(θ) = c²F(θ) 이 됩니다. 이렇게 차원 해석을 했을 뿐이지만, 피타고라스 정리가 증명된 것을 확인할 수 있습니다.

충격파 확산 모델

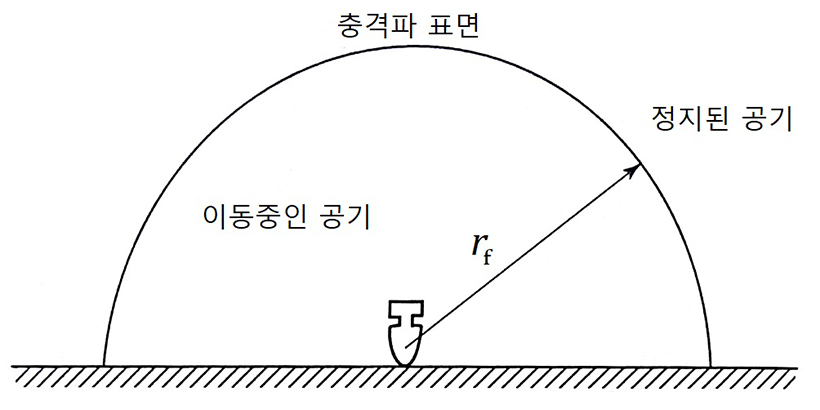▲ 대칭적인 구형 화염전파 수학 모델

영국의 물리학자 테일러는 시간 경과에 따른 충격파 확산 반경을 산정하는 모델을 연구했습니다. 그는 충격파 반경 R은 폭발에너지 E, 공기 밀도 ρ, 그리고 시간 t 등에 의해서 결정된다고 생각했습니다. 엄밀하게는 초기폭발 크기와 대기압 등 다른 변수들이 있었지만 과감하게 무시했습니다. 왜냐하면, 시간이 조금만 지나도 충격파가 퍼져나간 반경은 초기 반경에 비해 훨씬 크다고 생각했기 때문입니다. 그는 변수를 R=f(E,ρ,t) 로 단순화했습니다. 이 변수 4개를 조합하면 Π=R¹E^-1/5ρ^1/5t^-2/5와 같은 무차원 변수가 한 개가 도출됩니다.

따라서 충격파 반경은 폭발에너지와 공기밀도가 일정한 경우, 시간에 따라서 2/5제곱에 비례해서 증가한다는 결론을 내리게 됩니다. 그는 실제 실험을 통해서 화염전파 반경을 측정하였고 결과를 검증했습니다. 또한, 이를 통해 간단한 차원해석을 통해서 공기 중에서 전파되는 강력한 충격파의 확산 반경을 설명하는 근사한 수학적 모델을 만들 수 있었습니다.

차원해석은 물리 현상이나 공학 문제를 결정하는 변수로부터 무차원 변수를 유도하고 변수들 사이의 관계를 분석할 수 있도록 해주기 때문에, 새로운 문제에 도전하는 경우 유용하게 쓰입니다. 문제접근 초기에 간단한 차원해석을 통해 전반적인 개념을 파악하고 운이 좋으면 문제를 설명하는 새로운 수학적 모델을 만들 수 있습니다. 차원해석을 이해하면서 사고의 차원도 함께 넓혀 나가기 바랍니다.