모든 공학 단위는 질량, 길이, 시간을 포함하는 7개의 기본 단위로부터 유도됩니다. 여기에 추가해서 물리적 차원을 갖지 않는 보조 단위가 2개 있는데, 바로 평면각(라디안)과 입체각(스테라디안)입니다. 평면각이란 두 직선이 이루는, 벌어진 정도 또는 회전의 정도를 의미합니다. 또 입체각은 3차원 공간에서 바라보는 면의 크기를 나타내는 입체적인 각도입니다.

평면각

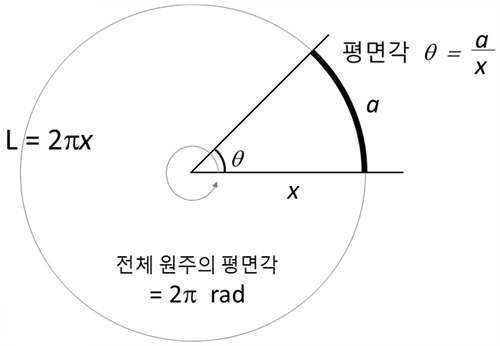
▲ 라디안의 정의

평면각을 표시할 때 주로 ‘도(degree)’를 사용하지만, 자연과학 분야에서는 호도법에 의한 라디안(radian)을 사용합니다. 호도법이란 호의 길이를 이용해서 각도를 표시하는 방법으로, 반지름(x) 대비 호의 길이(a)의 비율(θ=a/x)로 라디안을 정의합니다. 따라서 360도는 2π 라디안이고, 1라디안은 약 57도가 됩니다.

라디안 각도는 π가 나오고, 60도가 아닌 57도라는 숫자가 나오기 때문에 어렵게 느껴질 수 있습니다. 하지만 사각 모서리는 90도, 반대 방향은 180도와 같은 통상적인 각도는 우리가 익숙해서 그렇지, 한 바퀴를 360도로 정한 것이 오히려 인위적이라 생각할 수 있습니다.

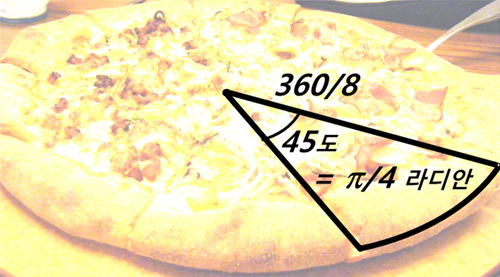
▲ 8개로 나눈 피자 한 조각의 각도

옛날 바빌로니아 사람들은 60진법에 근거한 숫자 체계를 좋아했습니다. 360은 1년 365일과 가까운 숫자이기도 하지만, 무엇보다도 2, 3, 4, 6 등 여러 숫자의 공배수가 되는 완전한 수로 여겨져 왔기 때문입니다. 사실 12까지의 수 가운데 7과 11을 제외한 모든 수로 나누어집니다. 따라서 피자 한 판을 여럿이 나누어 먹을 때 소수점 걱정을 하지 않아도 됩니다. 4명이면 90도, 6명이면 60도, 8명이면 45도로 나누면 됩니다.

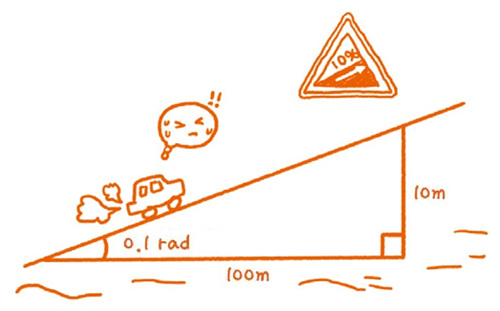
▲ 경사면 기울기와 라디안

라디안은 ‘거리 대비 원호 길이의 비’이고 차원이 없는 무차원 값이며, 기울기라는 직관적인 의미가 살아있습니다. 도로를 주행하다 보면 도로표지판에 경사도를 %로 표시해 놓은 것을 볼 수 있습니다. 경사도가 10%라고 하면 탄젠트 값이 0.1이란 의미입니다. 수평 방향으로 100m 갈 때마다 10m씩 올라간다는 말입니다. 수식으로 표현하면 10% = tan 0.1 ≈ sin 0.1 ≈ 0.1 rad 입니다.

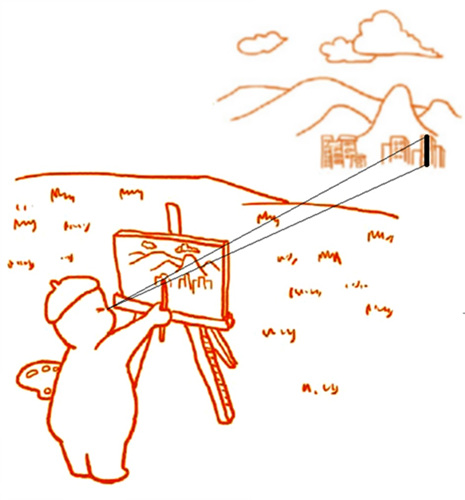
▲ 풍경화 (출처: 공대생이 아니어도 쓸데있는 공학이야기)

풍경화를 그릴 때 화가들은 한눈을 감고 한쪽 팔을 쭉 뻗은 채, 엄지손가락을 치켜들고 멀리 보이는 물체의 크기를 가늠합니다. 여기서 손을 앞으로 쭉 뻗었을 때, 눈에서 엄지손가락까지 거리를 약 60cm라 정하면, 1.5cm인 엄지손톱이 이루는 각도는 1.5/60, 즉 1/40 rad입니다. 예를 들어 먼 곳에 있는 사람이 엄지손톱만 하게 보인다면, 사람 키가 1.7m 정도이고, 그곳까지의 거리를 대략 1.7×40=68m로 계량할 수 있습니다.

입체각

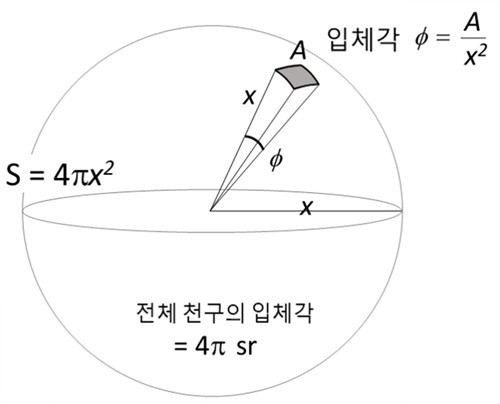
▲ 스테라디안의 정의

입체각은 평면각을 3차원으로 확장한 것으로, 눈으로 보이는 면적의 크기를 나타낼 때 사용합니다. 같은 물체라도 가까이 있으면 크게 보이고 멀리 있으면 작게 보입니다. 태양은 달보다 400배 크지만, 그만큼 멀리 있어서 우리 눈에는 둘 다 거의 같은 크기로 보입니다.

입체각은 스테라디안(sr)이라는 단위를 쓰며 라디안(rad)과 마찬가지로 무차원 단위입니다. 스테라디안은 면적의 크기(A)를 바라보는 거리(x)의 제곱으로 나눈 값(φ=A/x2)으로 정의합니다. 예를 들어 가로 세로가 a와 b인 직사각형인 경우, 입체각은 면적 ab를 거리의 제곱으로 나눈 값(ab/x2)입니다. 즉, 양방향 평면각(θ1=a/x, θ2=b/x) 두 개를 곱한 것으로 이해할 수도 있습니다.

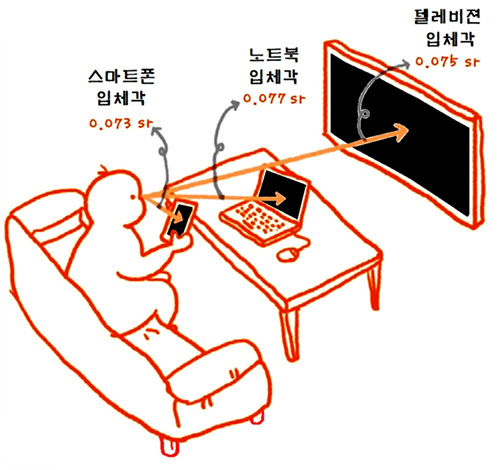
▲ 스크린 입체각 (출처: 공대생이 아니어도 쓸데있는 공학이야기)

우리는 여러 가지 크기의 스크린을 보면서 살고 있습니다. 스마트폰(7.1cm×12.6cm)을 35cm 거리에 두고 보면 입체각은 0.073sr이고, 15형(33cm×19mm) 노트북을 90cm에서 사용하면 0.077sr, 또 3m 떨어진 벽에 걸린 48형(104cm×65cm) 텔레비전을 보는 입체각은 0.075sr입니다. 작은 것은 가까이 보고, 큰 것은 멀리 놓고 보기 때문에 대체로 시야를 차지하는 화면의 크기가 모두 엇비슷한 것을 알 수 있습니다.

라디안과 스테라디안은 각도를 나타내기 위해 국제표준단위계에서 채용한 보조 단위로 무차원 값을 가집니다. 우리가 흔히 각도로 사용하는 도, 분, 초의 단위는 사실 비SI 단위입니다. 평면각과 입체각을 직관적으로 표시해주는 라디안과 스테라디안에 익숙해짐으로써, 도형 혹은 공간을 깊이 이해할 수 있고, 아울러 여러 유용한 활용 범위를 찾을 수 있을 것입니다.