
힘이 작용하면 물체는 변형하거나 운동하게 되는데, 정역학(靜力學, Statics)은 변형하거나 운동하지 않는 정적인 평형 상태만을 다루는 역학입니다. 그럼 이제부터 힘의 평형을 다루는 정역학을 살펴보겠습니다.
* 힘의 평형이란? 정지 또는 등속운동을 하는 물체에 작용하는 힘을 모두 합쳐 제로가 되는 상태
세 힘의 평형상태
힘의 평형(equilibrium)을 이해하려면 우선 힘에 대해 알아야 합니다. 힘은 벡터량(vector quantity)입니다. 벡터는 스칼라(scalar)와 달리 크기와 방향을 가지고 있습니다. 스칼라에서는 1 더하기 1은 2가 되지만, 벡터에서는 방향에 따라서 크기가 2가 될 수도 있고 0이 될 수도 있습니다.

예를 들어 줄다리기할 때 양쪽에서 당기는 힘의 크기가 같다면 평형상태가 되지만, 세 개의 방향에서 당길 경우 한 개의 힘이 나머지 두 개의 합력과 같아야 평형상태가 됩니다. 이때 세 힘의 크기와 마주 보는 각과의 관계는 아래와 같습니다.
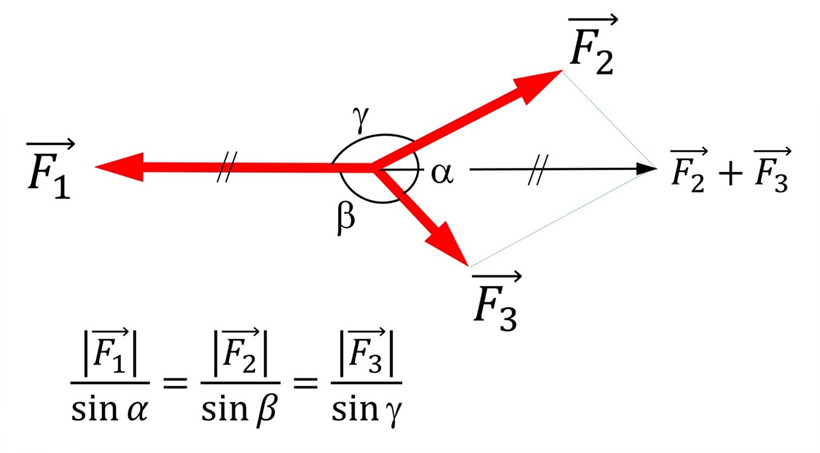
일반 줄다리기와 달리 크기가 다른 세 힘이 일직 선상에 있지 않더라도 평형을 이룰 수 있습니다. 여기서 재미있는 것은 가장 큰 힘이 나머지 두 개 힘의 크기를 합친 것보다 작거나 같으며, 두 힘의 방향에서 가장 먼 방향을 향한다는 사실입니다. 반대로 이야기하면 크기가 작은 두 개의 힘은 서로 가까이하며, 반대쪽에 있는 큰 힘에 대항하면서 평형을 이루는 것으로 이해할 수 있습니다.

예를 들어 세계 강국인 미국·중국·러시아의 국제 관계를 살펴보면 국력에 따라서 서로 가깝게 또는 멀리 친소 관계를 만들어 가면서 국제적인 힘의 평형을 유지해 왔습니다. 또한 선거 운동과정에서도 세 정당 후보가 나왔을 때 서로 경쟁하고 협력하는 모습도 힘의 평형으로 설명될 수 있습니다.
알기 쉽게 표현 가능한 ‘자유물체도’

정역학에서 힘의 평형을 해석하기 위해서는 자유물체도(free body diagram)를 이용해야 합니다. 자유물체도란 관심의 대상이 되는 물체를 분리해 놓고, 여기에 작용하는 힘을 독립적으로 표시한 그림입니다. 자유물체도를 이용하면, 아래 그림과 같이 경사면을 따라 자동차가 등속운동을 할 때 작용하는 마찰력과 중력 등을 알기 쉽게 표현할 수 있고, 필요한 추진력을 계산할 수 있습니다.
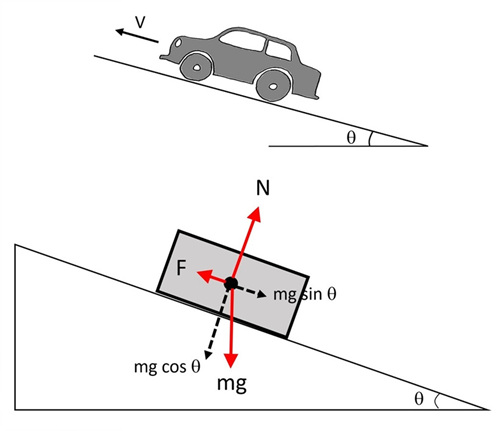
▲ 경사면을 오르는 자동차의 자유물체도
서로 맞닿아있는 물체에 힘이 작용하면 반대 방향으로는 반작용이 발생합니다. 때문에 자유물체도는 관심이 있는 대상을 중심으로 생각하고 분리해야 합니다. 관심 대상이 어느 쪽이냐에 따라 힘이 작용하는 방향이 반대가 되기 때문입니다.
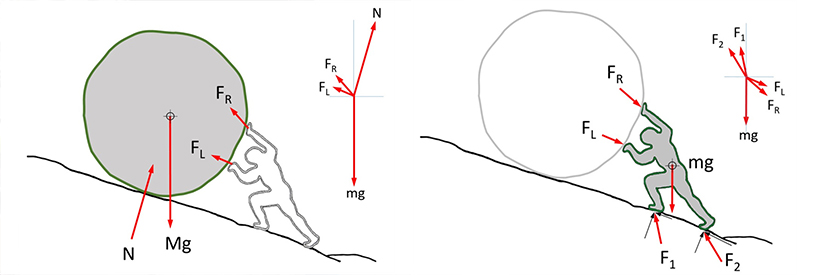 ▲ (왼쪽부터) 관심 대상이 돌멩이/인체를 중심으로 한 자유물체도
▲ (왼쪽부터) 관심 대상이 돌멩이/인체를 중심으로 한 자유물체도
위 그림과 같이 비탈에서 굴러 내려오는 돌멩이를 대상으로 힘의 평형을 생각할 수도 있고, 굴러 내려오는 돌을 막고 서있는 사람을 중심으로 자유물체도를 생각할 수도 있습니다.
‘힘의 모멘트’를 고려하라

힘의 평형을 이루기 위해서는 힘의 모멘트(moment of force)가 제로 상태이어야 합니다. 힘의 모멘트란 임의의 점을 중심으로 한 팔의 길이(힘의 작용선까지의 거리)와 힘의 크기의 곱으로 정의됩니다. 모든 힘이 하나의 질점(material point)에 작용하는 경우 힘의 모멘트를 고려할 필요가 없으나, 일정한 크기를 갖는 물체에 대해서는 힘의 모멘트도 고려해야 합니다. (*질점(material point)이란? 역학적으로는 질량을 갖고 있으면서 부피가 없는 물체를 말한다. 그러나 실제로는 어떤 물체나 부피가 있으므로 질점은 이상적으로만 존재한다.)
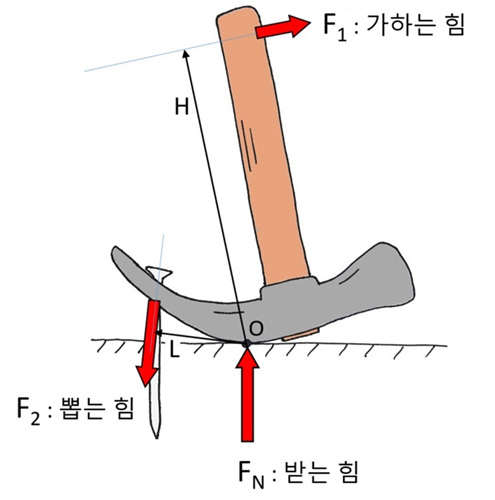
정역학은 물체에 작용하는 힘을 중심으로 사물을 관찰하면서 내부적으로 발생하는 힘의 크기와 방향을 가시화합니다. 힘의 평형 원리를 적용하여 트러스 등 각종 구조물의 접점을 중심으로 각 부재에 작용하는 작용과 반작용을 해석합니다. 이렇게 구한 힘의 크기와 방향을 근거로 재료역학(http://news.samsungdisplay.com/15816)적인 측면에서 재료의 강도나 변형을 해석하게 됩니다.

또한 물체가 정지해 있는 상태에서 정역학적인 해석은 운동하는 상태를 해석하기 위한 출발선이 됩니다. 따라서 정역학은 변형해석을 위한 재료역학과 운동 해석을 위한 동역학의 기초가 된다고 할 수 있습니다.
이처럼 정역학은 다양한 역학에 기초가 될 수 있으며, 앞으로도 이점은 변치 않을 것입니다. 공학의 기본 이론을 설명하는 ‘쉽게 알아보는 공학이야기’ 다음 편 동역학도 기대해주세요.

