
최근 어느 방송 예능 프로그램에서 유명 연예인이 진자를 이용한 그림 그리기, 즉 ‘펜듈럼 페인팅(pendulum painting)’을 선보여 화제가 되기도 했다. 진자란 고정점에 줄로 매달린 추로서 자유롭게 줄을 타고 왔다 갔다 할 수 있는 물체이다. 추에서 페인트가 흘러나와 추가 움직이는 대로 바닥에 페인트가 궤적을 남기면 진자가 그린 그림이 된다. 이때 진자가 규칙적인 운동을 하기 때문에 그 결과로 나온 그림도 규칙적이고 기하학적인 패턴을 나타낸다.
뉴턴역학과 진자운동

진자의 규칙성을 처음 발견한 사람은 그 유명한 이탈리아의 갈릴레오 갈릴레이다. 갈릴레오는 피사대학 의학부에 다니던 시절 피사 대성당에 매달려 있던 샹들리에가 이리저리 흔들리는 모습을 보고 놀라운 규칙성을 발견했다. 갈릴레오는 의대생답게 자신의 맥박을 이용해 샹들리에가 한쪽 끝에서 다른 쪽 끝까지 갔다가 다시 원위치로 돌아오는 데에 걸리는 시간(이를 주기라 한다)이 그 진폭과 무관하게 일정함을 알아냈다. 이후 갈릴레오는 진자의 주기가 추의 질량과도 무관함을 알아냈는데, 이처럼 진자의 주기가 진폭이나 질량과 무관한 성질을 등시성(isochronism)이라 한다. 진자의 주기에 영향을 주는 유일한 요소는 진자의 길이이다. 길이만 정해지면 진자의 주기가 결정된다. 그렇다면 진자는 아주 훌륭한 시계로 사용할 수 있다.

진자의 주기가 진폭이나 추의 질량과 무관하다는 사실은 언뜻 직관적으로 받아들이기 쉽지 않다. 진자의 한 예로 그네를 들 수 있다. 그네를 뛸 때 거의 제자리에서 타는 것과 한껏 뒤로 가서 타는 것은 다를 것 같지만, 사실 주기는 똑같다. 또한 체중이 무거운 사람이 탈 때와 가벼운 사람이 탈 때의 주기도 다를 것 같지만, 이것은 사실이 아니다. 이는 근본적으로 무거운 물체와 가벼운 물체가 똑같이 자유낙하한다는 원리와 같다.
진자의 주기가 오직 그 길이에만 의존한다는 사실은 뉴턴역학을 이용하면 간단하게 보일 수 있다. 진자의 진폭이 크지 않아서 추가 훑고 지나가는 경로의 길이가 진자의 길이에 비해서 대단히 짧을 때 진자의 운동방정식은 수학적으로 용수철에 매달려 왕복 진동운동을 하는 추의 운동방정식과 완전히 똑같다. 이때 진자의 운동방정식은 정확하게는 진자가 연직방향과 이루는 각도에 대한 2계 미분방정식이다. 대학교 일반물리학 수준의 지식만 있으면 누구라도 간단하게 진자의 운동방정식을 쉽게 유도하고 또 풀 수도 있다. 그 결과는 삼각함수로서, 진자의 추가 연직선과 이루는 각도는 시간에 따라 커졌다 작아지는 과정을 반복하는데 그 정도가 삼각함수로 주어지며 반복되는 주기가 진자의 길이를 중력가속도(g=9.8m/s^2)로 나눈 값의 제곱근에 비례한다.
단진자와 이중진자 운동
진자의 주기가 그 길이와 밀접한 관련이 있다는 사실을 이용하면, 어떤 길이로부터 시간을 정하거나 반대의 시간으로부터 길이를 정할 수 있다. 실제로 프랑스에서 처음 미터법을 제정할 때 1미터를 반주기가 1초인 진자의 길이로 정하자는 제안이 있었다.
물론 여기에는 중력가속도가 항상 일정하다는 가정이 숨어 있다. 현실에서는 그렇지 않다. 우선 해수면에서 고도가 높아질수록 지구 중심에서 멀어지므로 중력가속도의 값이 작아진다. 또한 지구가 자전하고 있기 때문에 회전에 의한 원심가속도가 중력가속도를 감소하는 효과를 낳는데, 이 원심가속도는 위도에 따라 다르다. 이 사실을 이용하면 일정한 길이의 진자의 주기를 측정함으로써 특정 지점의 중력가속도를 측정할 수 있다.
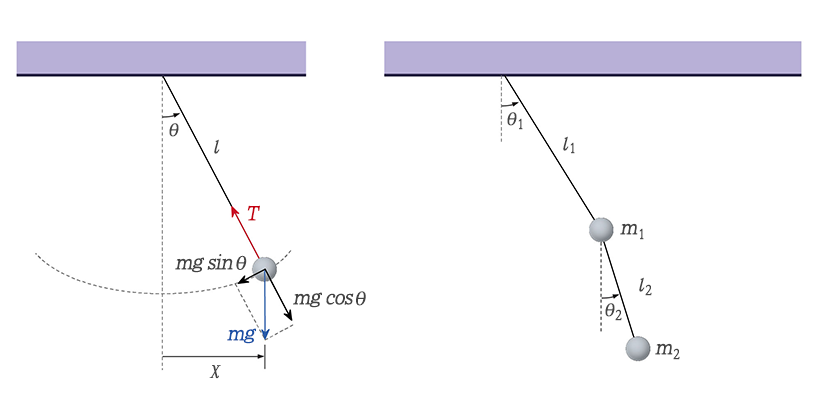
▲ ‘단진자’ (왼쪽)와 ‘이중 진자운동’(오른쪽)을 나타내는 그림
이처럼 추 하나가 줄 하나에 매달려 있는 진자를 단진자라 한다. 과학자들은 간단한 시스템에서 시작해 보다 복잡한 시스템을 만들기를 좋아한다. 단진자를 ‘가장 간단한 방식으로’ 복잡하게 만드는 방법은 단진자의 추 끝에 또 다른 단진자를 하나 매다는 것이다. 이를 이중진자(double pendulum)라 한다.
고정점에 바로 연결된 추를 추 1, 추 1에 연결된 추를 추 2라 하자. 이중진자는 추가 둘이고 줄도 둘이므로 이를 수학적으로 기술하려면 두 개의 변수가 필요하다. 즉, 추 1이 연직방향과 이루는 각도와 추 2가 연직방향과 이루는 각도로 변수를 잡을 수 있다. 단진자의 경우처럼 이 두 변수가 시간에 따라 어떻게 변하는지를 수학적으로 알면 이중 진자의 운동을 완벽하게 기술할 수 있다. 문제는 두 변수의 운동방정식을 쓰기가 쉽지 않다는 점이다.
▲ 이중진자 운동의 모습을 나타내는 시뮬레이션 영상 (출처: Paul Nathan 유튜브 채널)
운동방정식을 쉽게 구하는 방법 중 하나인 ‘라그랑지안 역학’

보통 물체의 운동을 기술할 때에는 어떤 정해진 축들을 기준으로 해서 좌표를 지정하고 그 좌표의 변화를 추적한다. 가장 흔하게는 3차원 공간 속에서 x, y, z 좌표를 잡을 수 있다. 복잡한 시스템이 복잡한 운동을 할 때에는 이런 기본적인 좌표보다 일반화된 좌표를 이용하는 것이 편리하다.
이때 일반화된 좌표에 대한 운동방정식을 쉽게 구하는 방법 중에 라그랑지안(Lagrangian)이라는 물리량을 이용하는 방법이 있다. 라그랑지안은 프랑스의 수리물리학자 조세프-루이 라그랑주(1736~1813)가 개발한 방법이다. 라그랑주는 10대부터 수학에서 두각을 나타낸 천재였고 수학과 역학, 천문학 분야에서 지울 수 없는 업적을 남겼다. 라그랑주가 살았던 18~19세기의 프랑스에서는 영국의 뉴턴역학을 수학적으로 보다 세련되게 가다듬고 체계적으로 정리하는 작업이 진행되었다. 라그랑지안을 이용한 그의 역학체계는 뉴턴의 고전역학을 매우 아름답게 재구성했을 뿐만 아니라 그 기본적인 방법론이 이후 현대물리학에까지 이어졌다. 필자가 연구하는 입자물리학 분야에서도 가장 중요한 출발점은 연구 대상의 라그랑지안을 찾는 것이다.
라그랑지안 역학의 핵심은 라그랑지안이라는 양을 구축하는 것이다. 이 양은 해당 시스템의 운동에너지 빼기 퍼텐셜 에너지로 주어진다. 고전적으로 운동에너지는 운동하는 물체가 갖는 에너지로 보통 질량 곱하기 속도의 제곱에 비례한다. 퍼텐셜 에너지는 그 시스템에 작용하는 힘과 관계된 에너지로서, 계에 작용하는 힘을 거슬러 그 계에 해 준 물리적 일의 양과 같다. 예컨대 바닥에 놓여 있는 공을 집어서 수직으로 들어 올리면 그 공은 위치에너지라는 퍼텐셜 에너지를 갖는다. 우리가 공에 작용하는 중력이라는 힘을 거슬러서 물리적인 일을 해 주었기 때문에 그만큼의 양이 퍼텐셜 에너지로 저장되었다고 볼 수 있다.
어떤 시스템의 라그랑지안을 구했으면 그로부터 운동방정식을 구하는 것은 거의 기계적인 계산으로 달성된다. 이때 필요한 방정식이 오일러-라그랑주 방정식(Euler-Lagrange Equation)이다. 수학적으로 오일러-라그랑주 방정식은 라그랑지안에 대한 2계 편미분방정식으로서, 라그랑지안을 시간으로 적분한 ‘작용(action)‘이라는 양이 극값(국소적으로 최대 또는 최소)을 갖게 하는 방정식이다. 이 오일러-라그랑주 방정식이 곧 그 시스템의 운동방정식이다.
라그랑지안 역학 속에 담긴 철학은 이렇다. 운동방정식을 구한다는 것은 해당 시스템이 시작점에서 종착점까지 어떤 경로를 따라 움직이는가를 결정하는 것과도 같다. 예컨대 서울에서 뉴욕까지의 비행기 항로는 지구 표면의 굴곡진 표면을 따라가는 최단 경로이다. 진자의 추가 지나가는 운동 궤적은 부채꼴 호의 일부 구간이다. 만약 그 호를 따라 왕복 운동하는 추의 끝에서 물감이 흘러나오게 하고 펜듈럼 페인팅처럼 그 아래 긴 종이를 일정한 속도로 지나가게 하면 종이 위에는 사인함수의 곡선이 그려져 있을 것이다. 이 곡선은 진자가 연직방향에서 벌어진 각도가 시간에 따라 어떻게 변하는지를 나타내는 운동방정식의 풀이에 해당한다.
최소작용의 원리로 만들어내는 아름다운 곡선

왜 하필 다른 곡선이 아니고 삼각함수일까? 라그랑지안 역학의 언어로 설명하자면 삼각함수가 진자라는 시스템의 작용을 최소화하는 경로이기 때문이다. 항공사에서 비행기 항로를 잡을 때 지표면의 굽은 곡면을 따라가는 최소경로를 선택한다면, 진자는 자신과 결부된 작용을 최소화하는 경로를 선택한다. 그 경로를 찾아주는 마법의 방정식이 바로 오일러-라그랑주 방정식이다.
놀랍게도 이는 진자에만 적용되는 원리가 아니다. 모든 물리계는 자신과 관련된 작용을 극대로 만드는 경로를 따라 운동한다. 사람은 최단거리에 해당하는 경로를 선택하고, 물리계는 작용을 최소(또는 극대)로 하는 경로를 선택한다. 이를 최소작용의 원리(Principle of least action), 또는 정적인 작용의 원리(Principle of stationary action)라 한다. 이는 마치 물리계가 가능한 모든 경로들 중에서 작용을 최대나 최소로 만드는 경로를 이미 알고 있거나 정확하게 골라내는 경이로운 능력이 있는 것처럼 보인다.
이와 비슷한 경우를 ‘페르마의 원리’에서도 찾아볼 수 있다. 페르마의 원리란 빛의 이동경로가 소요시간을 최소로 하는 경로에 해당한다는 원리이다. 예컨대 공기 중에서 물속으로 빛이 진행할 때 공기와 물의 경계면에서 굴절하게 되는데, 이렇게 꺾인 경로를 따라가야 서로 다른 두 매질을 지나갈 때 걸리는 총 소요시간이 최소이다. 테드 창의 소설 <네 인생의 이야기>를 영화로 만든 <콘택트(Arrival)>에서는 외계인의 언어를 이해하는 모티브로 페르마의 원리가 등장하기도 한다.
뉴턴역학과 라그랑지안 역학의 차이점은 무엇일까?
▲ 진자 운동의 원리가 숨겨진 펜듈럼 페인팅 (출처: Art Insider 유튜브 채널)
뉴턴역학으로 문제를 푼다는 것은 뉴턴의 운동 제2법칙, 즉 그 유명한 F=ma를 푸는 것이다. 일단 이 방정식을 구성하려면 해당 시스템에 작용하는 모든 힘(F)과 가속도(a)를 알아야 한다. 이중진자처럼 시스템이 복잡해지면 이 방법이 쉽지 않을 수도 있다.
반면 라그랑지안 역학에서는 해당 시스템의 운동에너지와 퍼텐셜 에너지부터 구한다. 그 차이가 곧 그 시스템의 라그랑지안이다. 이중진자의 경우 추 1과 추 2의 운동에너지 및 퍼텐셜 에너지를 각각 구해서 (두 운동에너지의 합) 빼기 (두 퍼텐셜 에너지의 합)을 구하면 이중진자의 라그랑지안을 얻는다. 여기에 오일러-라그랑주 방정식을 적용하면 연직방향에 대한 두 추의 각도를 나타내는 두 변수에 대한 미분방정식을 얻는다. 이 자체가 운동방정식이다. 이제 이 방정식을 각 변수에 대해 풀면 최종적인 결과가 나온다.
단진자의 경우 뉴턴역학을 적용해 F=ma를 써서 곧바로 운동방정식을 쉽게 얻을 수 있다. 물론 단진자에서도 운동에너지와 퍼텐셜 에너지를 구해 라그랑지안을 구축하고 거기에 오일러-라그랑주 방정식을 적용해도 똑같은 방정식을 얻는다. 이중진자의 경우에는 라그랑지안 역학이 훨씬 쉽다. 특히 이렇게 구한 이중진자의 운동방정식은 두 변수가 복잡하게 뒤얽힌 2계 미분방정식이다. 단진자의 경우처럼 두 추가 움직이는 각도가 충분히 작을 때에는 방정식을 쉽게 풀 수 있다. 일반적인 각도가 아닐 때에는 해석학적으로 이 방정식을 풀 수가 없다. 남은 방법은 수치적으로 방정식의 풀이를 구해보는 것이다.
이중진자는 혼돈계(chaotic system)의 하나로 알려져 있다. 혼돈계에서는 초기조건에 아주 작은 변화를 주었을 때 최종적인 결과가 대단히 증폭해서 나타난다. 혼돈계는 원리적으로는 결정론적으로 예측가능한 시스템이지만 시간에 따른 오차의 효과가 기하급수적으로 증가해 실질적인 예측은 사실상 어렵다. 따라서 이중진자로 그림을 그린다면 단진자의 경우와 달리 대단히 복잡하면서도 예측하기 어려운 패턴을 얻을 수 있다.
※ 이 칼럼은 해당 필진의 개인적 소견이며 삼성디스플레이 뉴스룸의 입장이나 전략을 담고 있지 않습니다.



