
이런 문제를 어떻게 푼다고? 바로 ‘페르미 추정법’으로 풀자!
우리나라에서 하루에 팔리는 치킨은 몇 마리일까? , 시카고에 있는 피아노 조율사는 모두 몇 명일까?, 서울에 있는 미용실은 몇 곳일까? 이런 질문에 선뜻 답하기 쉽지 않다. 하지만 잠깐만 수학적으로 생각한다면 어렵지 않게 답을 얻을 수 있다.

우선 첫 번째 질문에 대한 답을 구해 보자. 과연 하루에 팔리는 치킨은 몇 마리일까?
현재 우리나라 인구는 약 5000만 명이고, 2~3명이 한 가구를 이룬다고 가정하면 우리나라 전체 가구 수는 약 2000만이다. 한 가구당 평균적으로 얼마나 자주 치킨을 주문할까? 하루 한 번은 너무 잦고, 한 달에 한 번은 너무 드무니 대략 일주일에 한 번 정도 주문한다고 가정하자.
그러면 일주일에 2000만 마리의 치킨이 팔리고, 일주일은 7일이므로 하루에 팔리는 치킨은 2000만을 7로 나눈 값이다. 즉, 20,000,000÷7≈2,857,00이므로 평균적으로 하루에 약 290만 마리의 치킨이 팔린다고 할 수 있다.
나아가 이 추측으로부터 우리나라에 있는 치킨집의 수도 알 수 있다. 치킨집이 유지되기 위해서는 적당한 이익이 보장되어야 하는데, 하루에 10마리 정도만 팔린다면 치킨집은 문을 닫을 것이다. 그렇다고 하루에 1000마리 정도를 튀겨낼 수 있는 치킨집은 많지 않을 것이다.
그래서 하루에 평균적으로 50마리 정도 팔린다고 가정할 수 있고, 이 치킨집이 일주일에 6일 영업한다면 한 가게당 일주일에 300마리의 치킨을 공급할 수 있다. 그런데 일주일에 2000만 마리가 필요하므로 20,000,000÷300≈67,000이다. 즉, 우리나라에는 약 67,000개의 치킨집이 있다고 추정할 수 있다.
그런데 2019년 6월 3일에 한국경제신문의 보도에 따르면 우리나라에 있는 치킨집 수는 8만 7000개 (2019년 2월 기준)이다. 약 2만 개 정도 차이는 있지만, 이 정도면 훌륭한 근삿값이다. 왜냐하면 약 2만 개의 치킨집은 손해를 볼 수밖에 없는 치킨이 거의 팔리지 않는 집일 수 있기 때문이다.
현상의 본질을 꿰뚫어 핵심만 얻는 페르미 추정의 기원과 역사
 ▲ 최초의 원자로를 만든 핵물리학자 ‘엔리코 페르미’ (출처: https://www.greelane.com/)
▲ 최초의 원자로를 만든 핵물리학자 ‘엔리코 페르미’ (출처: https://www.greelane.com/)
페르미 추정(Fermi Estimate)’이라고 하는 이와 같은 문제해결 방법은 1938년 노벨 물리학상을 받은 이탈리아계 미국 물리학자인 엔리코 페르미(1901~1954)로부터 기인했다. 페르미 추정을 ‘게스티메이션(Guesstimation)’이라고도 한다.
그는 1942년 최초로 인공적인 핵반응로 실험에 성공했고, 1944년부터 핵무기 개발계획인 ‘맨해튼 프로젝트’를 수행했던 미국 로스앨러모스 연구소의 부소장으로 핵무기 개발을 지휘했다. 2차 대전이 막바지로 치닫던 1945년 7월 16일에 미국 뉴멕시코주 사막 한가운데서 사상 최초의 핵무기 폭발 실험이 진행되었다.

그날 폭심에서 약 10㎞ 떨어진 베이스캠프에 있던 페르미는 실험용 폭탄이 터질 때 그 위력이 어느 정도인지 간단한 실험으로 추측했다. 페르미는 핵폭탄이 터지자 종잇조각을 찢어 폭발로 일어난 바람에 날려 보냈다. 그는 다음과 같이 추정했다고 밝혔다.
‘폭발 후 약 40초가 지나자, 폭풍이 내게 닿았다. 나는 충격파가 지나가기 이전, 도중, 나중에 각각 작은 종잇조각을 약 1.8m 높이에서 떨어뜨려 그 폭발력을 추정해봤다. 그때 마침 바람이 불지 않았기에, 나는 폭풍이 지나가는 도중에 떨어진 종이 조각의 변위를 명확하고 사실적으로 측정할 수 있었다. 변위는 약 2.5m 정도였고, 그때 나는 이 정도의 폭풍이면 TNT 1만 톤의 폭발 위력에 해당한다고 추정했다.’
페르미는 잠깐의 계산으로 핵폭탄의 위력이 TNT 1만 톤이라는 것을 알아냈다. 실제로 이 실험에서 핵폭탄의 정확한 폭발력은 TNT 1만 8600t이었다고 한다.
기초적 지식과 논리적 추론을 통해 근삿값을 얻어내다.

페르미 추정은 1940년 어느 날 수업에서 시작되었다. 페르미는 시카고대학에서 강의 중에 학생들의 사고력을 기르기 위해 “시카고에 사는 피아노 조율사는 몇 명일까?”라는 문제를 냈다. 학생들이 이 문제에 답을 못하자 페르미는 우선 다음과 같이 가정했다.
① 시카고의 인구는 약 300만 명이다.
② 가구당 구성원은 약 3명이다.
③ 피아노 보유율을 10% 정도라 하자.
④ 피아노 조율은 일 년에 한 번 한다고 가정한다.
⑤ 조율사가 조율에 걸리는 시간은 이동 시간을 포함해 2시간 정도이다.
⑥ 조율사는 하루 8시간, 주 5일, 1년에 50주간 일한다.
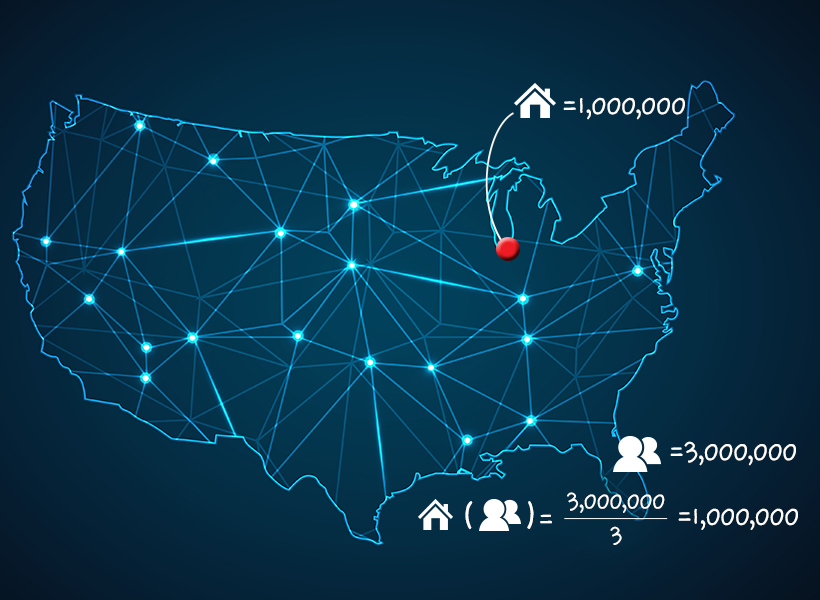
페르미는 이런 가정을 바탕으로 다음과 같이 대략적인 피아노 조율사의 수를 추론하였다.
❶ 인구는 300만이고 3명이 한 가구를 이루므로 시카고에는 약 100만 가구가 있다. (3,000,000÷3=1,000,000)
❷ 피아노 보유율이 10%이므로 시카고에 있는 피아노는 약 10만 대이다. (1,000,000×10/100=100,000)
❸ 피아노 조율은 일 년에 한 번 한다고 가정했으므로 시카고의 피아노 조율은 연간 10만 건이다.
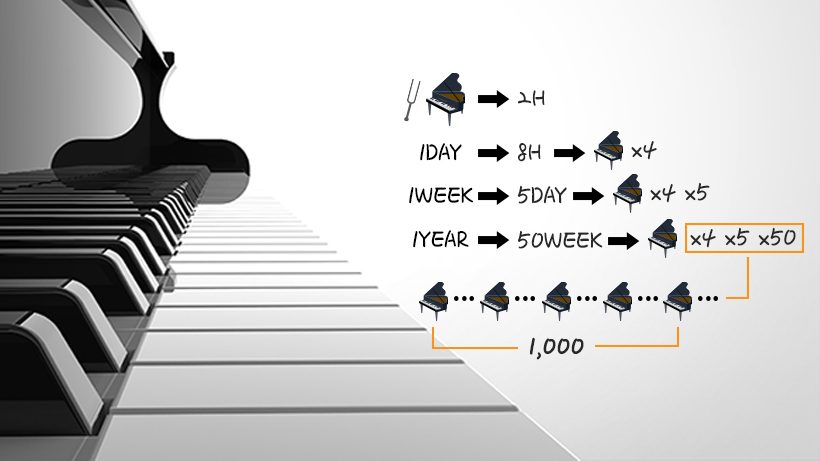
❹ 피아노 조율사는 피아노 한 대를 조율하는데 2시간 걸리고, 하루에 8시간 일하므로 하루에 4대의 피아노를 조율할 수 있다.
❺ 조율사는 주 5일, 1년에 50주를 일하므로 조율사 한 명이 1년에 조율할 수 있는 피아노는 1000대이다.
❺ 따라서 시카고에 있는 피아노 조율사의 수는 100명이다. (100,000÷1,000=100)
페르미가 얻은 피아노 조율사 수의 근삿값은 당시에 실제 시카고 전화번호부에 있는 수와 비슷했다고 하니 아주 얼토당토않은 추정은 아니었음을 알 수 있다. 이처럼 페르미 추정은 기초적인 지식과 논리적 추론을 통해 짧은 시간에 근삿값을 얻는 수학적 과정이다.
최소한의 조건을 통해 논리적으로 문제를 해결해 나가자!

이제 페르미 추정으로 앞에서 질문했던 ‘서울에 있는 미용실은 몇 곳일까?’를 해결해보자. 우선 페르미처럼 몇 가지 가정이 필요하다.
① 서울의 인구는 약 1000만 명이다.
② 한 달에 한 번씩 미용실에 간다.
③ 미용실은 일주일에 한 번 쉬고, 한 달에 26일 일한다.
④ 한 미용실에 미용사 평균 3명이다.
⑤ 한 미용사는 한 시간에 2명의 머리를 다듬는다.
⑥ 미용사는 하루에 10시간 일한다.
위의 가정에서 한 달에 미용실에서 받는 손님은 1000만 명이고, 한 미용실에서 받을 수 있는 손님은 3×2×10=60명이다. 한 미용실에서 받을 수 있는 한 달 동안의 손님은 60×26=1,560명이다. 따라서 서울에 있는 미용실의 수는10,000,000÷1,560≈6,410이다. 즉, 서울에는 약 6,500개의 미용실이 있다고 추측할 수 있다.
페르미 추정은 치킨의 판매량, 미용실의 수, 어떤 집회에 참여한 사람 수와 같이 단순한 생활 문제에만 활용할 수 있는 것은 아니다. 요즘 지구 온난화 때문에 크고 작은 기후변화로 지구는 몸살을 앓고 있는데, 지구 온난화의 주범은 인간이 만들어 낸 이산화탄소 때문이다. 우리는 기상학자나 환경전문가는 아니지만, 우리가 가지고 있는 기초지식만을 활용한 페르미 추정으로 대기 중 이산화탄소가 얼마나 증가했는지 대강 알 수 있다.

우리가 하루에 식사로 얻는 에너지는 약 2,000kcal라고 한다. 그런데 우리에게 필요한 것은 음식을 통한 에너지만은 아니다. 자동차도 타야 하고, 전기도 사용해야 하고, 물건도 만들어야 한다. 그래서 한 사람이 하루에 소비하는 모든 에너지를 합한 평균을 식사로부터 얻는 에너지의 50배인 약 100,000kcal이라고 가정하자.
2020년 6월 현재 세계에는 약 77억 명이 살고 있으므로 하루에 소비되는 전 세계 에너지는 7,700,000,000×100,000= 7.7×1014kcal이다.
탄수화물로 이루어진 에너지바 하나로 얻을 수 있는 에너지는 약 100kcal이다. 탄소는 탄수화물의 일부이고, 산소와 결합하여 이산화탄소가 되는데 이때 약 10g 정도의 이산화탄소가 배출된다고 가정하자.
즉, 에너지 100kcal 당 10g의 이산화탄소가 배출된다. 그러면 하루 동안 전 세계에서 소비되는 에너지는 7.7×1014kcal이므로 하루 동안 7.7×1013g의 이산화탄소가 배출됨을 알 수 있다. 1년은 365일이므로 연간 7.7×1013×365≈2.8×1016g의 이산화탄소가 배출된다. 그런데 과학자들의 연구에 의하면 1958년부터 반세기에 걸쳐서 대기 중의 이산화탄소 농도의 변화를 정밀하게 관측한 결과, 대기 중에 이산화탄소가 연간 약 1016g의 비율로 증가하고 있다고 한다. 즉, 우리의 추정이 얼토당토않은 것은 아니라는 결론을 얻을 수 있다.

이처럼 페르미 추정은 정확한 답을 위한 것은 아니고, 제시된 문제를 최소한의 조건에서 답을 얼마나 논리적으로 찾는지 그 과정을 알아보는 것이다. 페르미 추정은 미적분과 같은 고도의 수학적 내용을 필요로 하지 않고, 초등학교에서 배운 간단한 산술과 기본 상식이면 충분하다.
이를 이용해 짧은 시간에 논리적인 가설과 가정을 통해 대략적 추정치를 얻어 활용하는 데 의미가 있다. 이때 알고 있는 정보가 많을수록 유리하므로 페르미 추정은 ‘아는 정보를 최대한 활용해서 새로운 정보를 생산’하는 것이다.
말년에 페르미는 안타깝게도 암에 걸려 세상을 떠났다. 그는 병상에 누워서도 링거의 물방울이 떨어지는 간격을 측정해 링거의 유속을 계산했다는 일화로도 유명하다. 죽음을 앞두고도 추론을 멈추지 않았던 페르미가 평생 강조한 것은 제한된 시간과 부족한 자료만으로도 답을 찾아가는 ‘논리적 사고력’이었다.
오늘날 세상은 하루가 다르게 빠르게 변하고, 빠른 변화에 따라 불확실성은 점점 커지고 있다. 이런 상황에서 페르미 추정을 활용하면 누구나 알고 있는 간단한 상식으로부터 신속하게 불확실성을 줄여줄 정보를 얻을 수 있고, 유익한 추론을 빠르게 할 수 있다.
물론 정확한 추론은 통계로 엄격하게 검증해야 하지만 빠른 결정과 시시각각 변하는 5G 시대에 적응하기 위해서 페르미 추정은 매우 훌륭한 휴대용 정보 추출기라고 할 수 있다. 이런 정보 추출기는 우리 모두의 머릿속에 있지만, 바로 지금 우리가 그것을 사용하고 있는지 아니면 녹슬게 놔두고 있는지 생각해 볼 문제다. 혁신의 시작은 바로 이와 같은 수학적 추론으로부터 시작되기 때문이다.
※ 이 칼럼은 해당 필진의 개인적 소견이며 삼성디스플레이 뉴스룸의 입장이나 전략을 담고 있지 않습니다.

