
안다는 것과 모른다는 것의 상태를 어떻게 정량화할 수 있을까요? 이는 정보 공학의 핵심 주제입니다. 우리는 정보화 시대에 살면서 다양한 방면에서 정보를 활용합니다. 그리고 정량화를 위해 통계열역학의 엔트로피 개념을 응용한 ‘정보 엔트로피’를 사용합니다. 정보 엔트로피는 정보를 저장하고 효과적으로 전송하는 정보통신 기술의 기초입니다. 또한 학습기구나 지식구조를 체계화하는 인공지능 기술의 이론적 토대가 되고 있습니다.
엔트로피 증가의 법칙
자주 사용되는 용어지만 '엔트로피' 개념은 늘 아리송합니다. 엔트로피는 자연 물질이 변형되어, 원래의 상태로 돌아갈 수 없는 현상을 말합니다. 흔히 '무질서도'라고도 말하는 엔트로피는 원래 온도, 압력, 엔탈피 등과 같은 열역학적 성질의 하나로, 열전달량을 절대온도로 나눈 값으로 정의됩니다. 열역학 제2법칙은 고립된 시스템의 엔트로피를 항상 증가하는 방향으로 진행된다고 설명합니다. 즉, 뜨거운 곳에서 차가운 곳으로 열이 전달되는 것처럼 자연현상과 시간의 방향성을 가리킵니다.
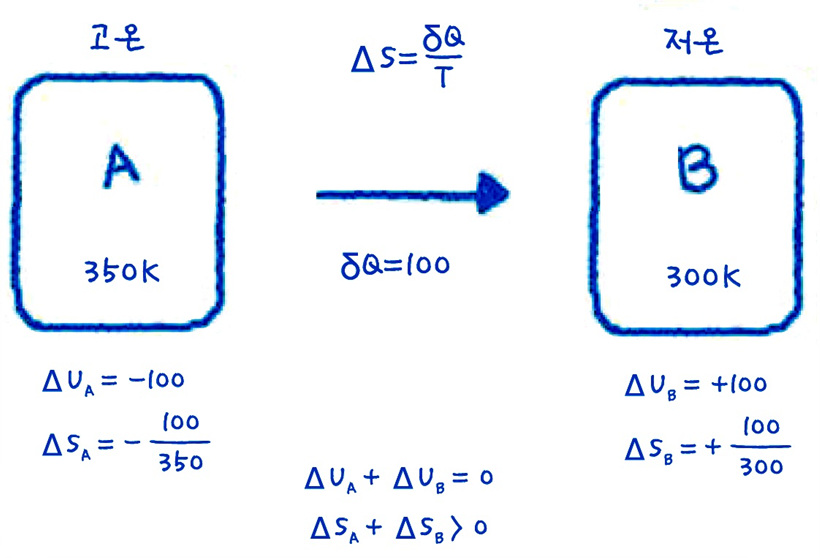 ▲ 두 물체의 에너지와 엔트로피 변화 (출처: 공대생도 잘모르는 공학이야기)
▲ 두 물체의 에너지와 엔트로피 변화 (출처: 공대생도 잘모르는 공학이야기)
자연현상은 자발적으로 두 물체 사이의 온도 차이가 사라지는 방향으로 일어납니다. 온도차가 없어지면서 더 이상 열전달이 이루어지지 않고, 아울러 에너지(available energy)를 사용할 수 없게 됩니다. 온도뿐 아니라 물에 잉크 방울을 넣거나, 두 기체 사이의 격리막을 제거하면 완전히 서로 섞여서 구별할 수 없는 상태가 됩니다.
엔트로피의 증가법칙이란, 변화를 유발하는 온도차나 물질 구분이 없어지면서 더 이상 변화가 일어나지 않는 상태로 진전됨을 의미합니다. 궁극적으로 우주의 모든 것은 균일화(homogeneous)되어 결국 아무것도 구별할 수 없는 혼돈의 상태, 즉 열적 죽음(thermal death)에 도달한다는 것이지요.
볼츠만의 엔트로피
통계열역학에서는 기체 분자의 확률 또는 경우의 수를 써서 엔트로피를 나타냅니다. 많은 수의 기체 분자들이 한 곳에 몰려 있을 확률보다 골고루 흩어져 있을 확률이 훨씬 높습니다. 질서정연하던 것이 저절로 무질서(disorder)해지는 것으로 볼 수도 있고, 반대로 균일화되는 과정으로 이해할 수도 있습니다.
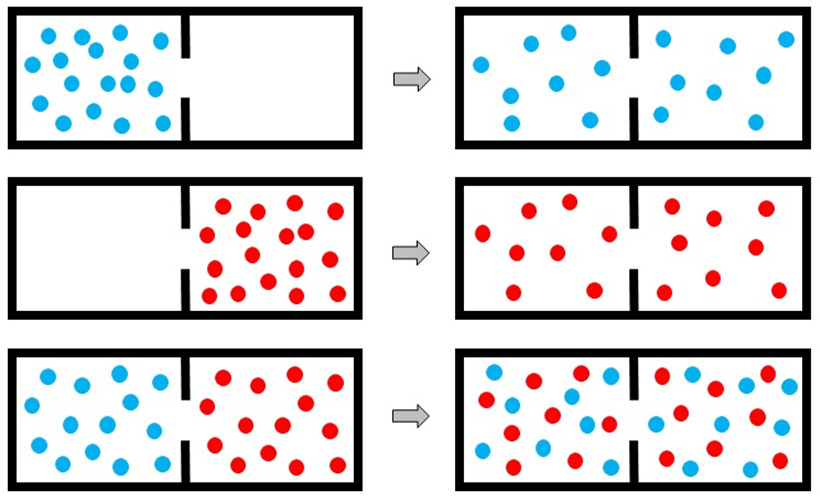 ▲ 기체 분자의 자발적인 확산과 혼합
▲ 기체 분자의 자발적인 확산과 혼합
볼츠만은 엔트로피를 기체 분자 거동에서 일어날 수 있는 경우의 수에 로그를 취한 값으로 정의했습니다. 하지만 그가 발표한 로그 공식은 동료 과학자들에게 인정을 받지 못했습니다. 그가 죽은 후에야 비로소 미시적인 분자 거동으로부터 거시적인 열역학 현상을 설명하는 이론으로 인정받게 됩니다.
정보 엔트로피
볼츠만의 엔트로피 개념은 정보이론의 토대가 됩니다. 미국의 전기공학자 섀넌은 <통신의 수학적 이론>이라는 논문에서 정보 엔트로피(information entropy)라는 개념을 제시했습니다. 그는 정보 엔트로피를 ‘미지의 정도’ 또는 ‘불확실성의 정도’로 규정하고 그런 일이 생길 수 있는 평균적인 로그 확률로 정의했습니다.
정보 엔트로피는 열역학 엔트로피처럼 경우의 수가 많은 상태가 엔트로피가 높은 상태가 됩니다. 경우의 수가 많다는 것은 확정적이지 않고, 확실하지 않은 상태를 의미합니다. 추가적인 정보가 주어지면 불확실한 상태에서 벗어나게 됩니다. 즉, 모름의 상태에서 앎의 상태로 넘어가면서 주어진 정보량만큼 정보 엔트로피가 감소하게 됩니다.
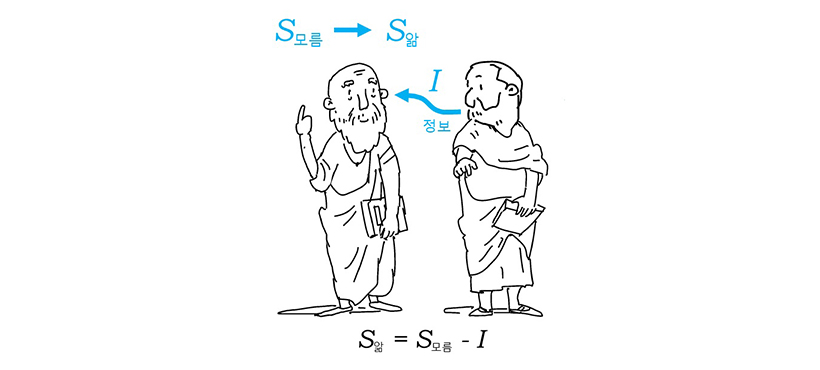 ▲ 앎과 모름의 정도를 나타내는 정보 엔트로피 (출처: 공학으로 세상을 말한다)
▲ 앎과 모름의 정도를 나타내는 정보 엔트로피 (출처: 공학으로 세상을 말한다)
엔트로피를 정의할 때 로그를 취하는 이유는 곱셈으로 늘어나는 경우의 수를 덧셈으로 바꿔주기 위함입니다. 동전 하나를 던질 때 나올 수 있는 결과는 앞면 아니면 뒷면이므로, 정보량은 1이고 경우의 수는 2입니다. 동전 2개를 던지면 정보량은 2개이고, 경우의 수는 4입니다. 즉 경우의 수는 거듭제곱에 따라 증가하므로, 로그를 취하면 정보량과 선형적인 관계로 바꿀 수 있습니다.
잘 알려진 놀이로 스무고개라는 것이 있습니다. 스무 번의 예/아니오 질문을 통해서 정답을 찾아가는 게임입니다. 경우의 수는 220, 즉 100만 경우가 됩니다. 즉 20비트의 정보를 가지면 거의 모든 문제의 정답을 맞출 수 있습니다. 물론 영리하게 질문하면 질문의 횟수를 줄일 수 있지만, 질문이 논리적이지 못하면 스무 번에 못 맞출 수도 있습니다. 중복되거나 불필요한 정보를 리던던시(redundancy)라고 하는데, 리던던시를 줄이면 적은 정보 속에서 좀 더 많은 양의 유용한 정보를 얻어낼 수 있습니다.
※리던던시(redundancy)란, 여분, 잉여라는 뜻으로 필요한 것보다 많거나 쓸데없이 중복되는 정보를 말한다.
무한 원숭이 이론

▲ 타자기를 두드리는 원숭이 (출처: 위키피디아)
원숭이가 무작위로 타자기 자판을 쳐서 셰익스피어 희곡을 만들 수 있을까요? 가능성은 매우 희박하지만, 무한성에 기초해서 슈퍼컴퓨터를 활용한다면 불가능한 것도 아니라는 얘기입니다. 단순한 예로 알파벳을 무작위로 조합해서 여섯 자를 만들어내는 경우를 생각해 봅니다.
알파벳은 26자이므로, 확률적으로 1/26의 6제곱입니다. 엔트로피로는 확률에 로그를 취한 값이므로, S=log2(1/26)6= 28비트가 됩니다. 알파벳 한 문자당으로 나누면 28/6= 4.7비트의 정보를 제공한 셈입니다. 하지만 실제 알파벳의 등장빈도는 동일하지 않습니다. 예를 들어 E, T, S는 실제 문장 중에 나타날 확률이 높고, Z, Q, J는 확률이 낮습니다. 각 알파벳의 발생확률을 고려해서 엔트로피를 계산하면 한 문자당 4비트 정도가 됩니다. 발생확률을 적용하는 것만으로 엔트로피를 줄인 것입니다. 이런 식으로 리던던시를 없애면서 정보 엔트로피를 줄여나가면, 원숭이가 셰익스피어를 쓰는 날이 예상했던 것보다 앞당길 수 있을 것입니다.
열역학의 엔트로피 개념은 통계열역학의 볼츠만 엔트로피로, 또 섀넌의 정보엔트로피로 학문 분야를 넘나들면서 발전해 왔습니다. 이제 정보 엔트로피는 전기신호의 처리와 송수신을 위한 정보통신공학을 넘어 자연어의 처리, 패턴의 인식, 신경망 회로, 학습의 과정, 언어학, 음악, 경제학, 사회학, 심리학, 교육학, 뇌공학, 의학, 생물학 등 전 학문 분야로 널리 확장 응용될 것입니다.

