막스 플랑크(Max Planck)는 양자역학의 성립에 핵심적인 기여를 한 독일의 물리학자로, 1899년 새로운 기본상수인 플랑크 상수(Planck Constant, 기호 ℎ)를 발견하였다. 그가 물리학계에서 최초로 ‘양자(Quantum)’라는 개념과 용어를 도입했기에 양자역학은 플랑크의 등장으로 시작되었다고 볼 수 있다.

플랑크 상수는 ℎ를 사용하며, 값은 ℎ = 6.63×10^-34 , 단위는 J·s이다. 숫자로 따지자면 10의 마이너스 34제곱이기 때문에 어마어마하게 작은 단위이다. 그만큼 양자의 크기가 작음을 느낄 수 있다.

플랑크 상수는 최근에 다시 한번 주목을 받았다. 그 동안 무게를 정의하기 위해 국제킬로그램(90%백금-10%이리듐 합금) 원기의 질량(1889년 정의)을 사용했으나, 작년 5월부터는 플랑크 상수를 질량의 기준으로 사용한다. 에너지 불연속 개념에서 도출된 플랑크 상수는 현세대에 연속성을 지닌 질량의 정의에 사용되는 기준이 되기도 한 것이다.

그럼 플랑크 상수란 무엇일까? 플랑크 상수는 고전 물리학의 골칫거리였던 흑체복사의 자외선 파탄 현상을 설명하려는 과정에서 시작됐다.

자외선 파탄현상에 관한 빈의 해석

플랑크는 자외선 파탄현상을 연구하며 흑체복사 강도의 분포에 관한 '빈의 공식(Wien's formula)'에 주목했다. 실험물리학자인 빈은 실험을 통해 공식을 만들었는데 흑체의 열복사 결과를 어느 정도 실제 값에 근사시켰다고 볼 수 있다.

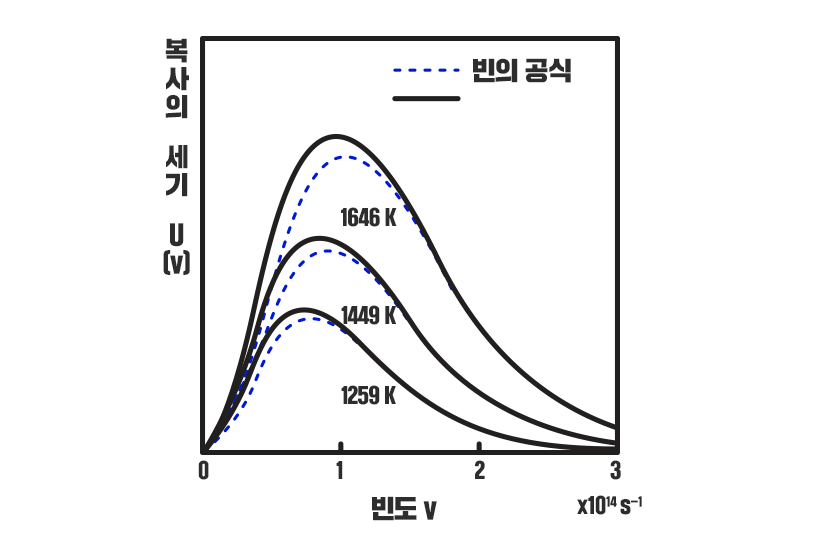▲ 빈의 공식을 이용한 복사에너지 근사

그래프상 약간의 오차를 가지고 있음을 알 수 있는데 도출 과정에서 고전물리학의 한계를 넘지는 못했기 때문이다. 이를 해결한 사람이 바로 플랑크이다.

플랑크의 해석

플랑크는 실험값으로 얻은 흑체 복사에너지를 단순히 데이터 회귀분석(regression analysis)를 통해 관계식을 도출하였다. 독립적인 연구이긴 하였으나, 결과적으로는 빈의 공식에 약간의 변형을 거친 형태인 평균 에너지의 분모항에 -1을 추가한 형태가 되었다. 실험치와 완벽하게 일치하는 공식을 유도해 낸 것이다.

수학적으로만 본다면, 플랑크의 수식은 아주 큰 파장의 공식을 다룬 레일리-진의 식과 아주 작은 파장을 다룬 빈의 식에 모두 수렴한다. 따라서 플랑크의 복사에너지 관계식이 전체 영역의 파장에 관하여 모두 설명 가능한 식이 된다.

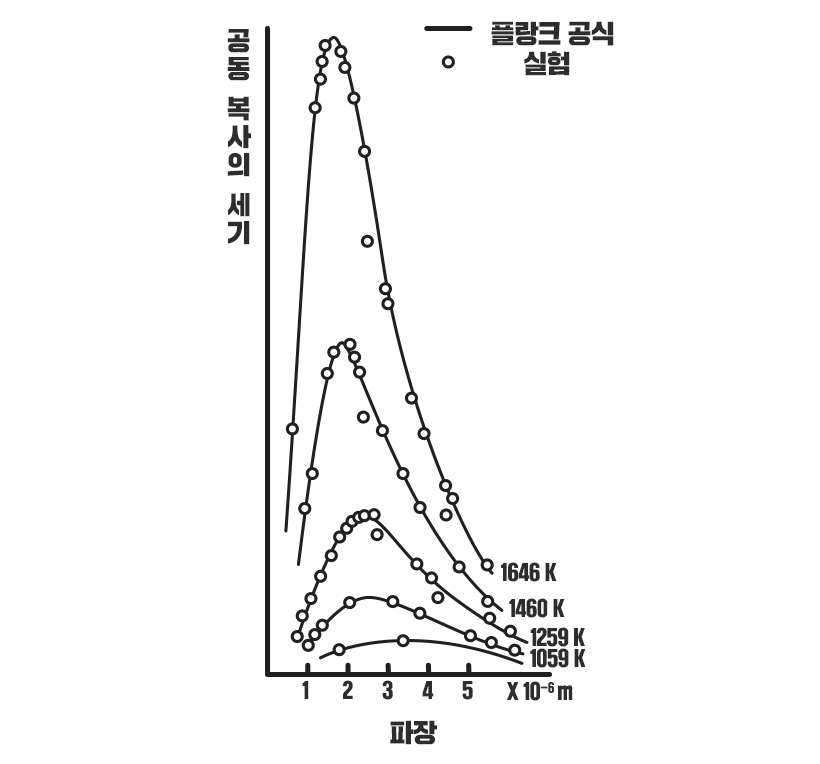▲ 플랑크의 곡선 회귀

이때 플랑크는 과감한 발상의 전환을 하게 되고, 자신이 믿고 있던 고전물리학의 개념에 위배되는 에너지의 양자화를 선언한다. 즉, 고전물리학 관점에서 보면 에너지는 연속적이며 프리즘을 통과한 무지개 또한 연속적이지만, 에너지를 불연속이고 나눌 수 있는 기본 단위체인 양자(Quantum)로 보자는 것이었다.

에너지 양자가설을 통한 플랑크 상수 도출

플랑크는 연속적인 에너지를 일정한 크기로 잘라서 단편화시킨 에너지 '양자가설(Quantum Hypothesis)'을 제안한다.

양자가설의 첫 번째 가정은 진동자(전자 등)의 에너지는 특정의 불연속 값을 갖는다는 것으로, 각 진동자는 식에 의해 불연속 값만을 가지므로 에너지가 양자화되었음을 의미한다. 두 번째 가정은 진동자는 한 상태에서 다른 상태로 전이할 때만 에너지를 흡수하거나 방출하며, 이때도 흡수/방출되는 에너지는 양자화된 값이다. 따라서 플랑크 이론의 중심은 에너지 상태의 양자화(Quantization)이다.

이는 추후 아인슈타인의 광양자설과 보어의 원자모형의 기본원리가 된다. 이처럼 양자역학은 가설을 바탕으로 시작해 실험으로 증명하고, 실험적인 현상을 다시 가설로 제안하는 과정에서 발전해 왔다.

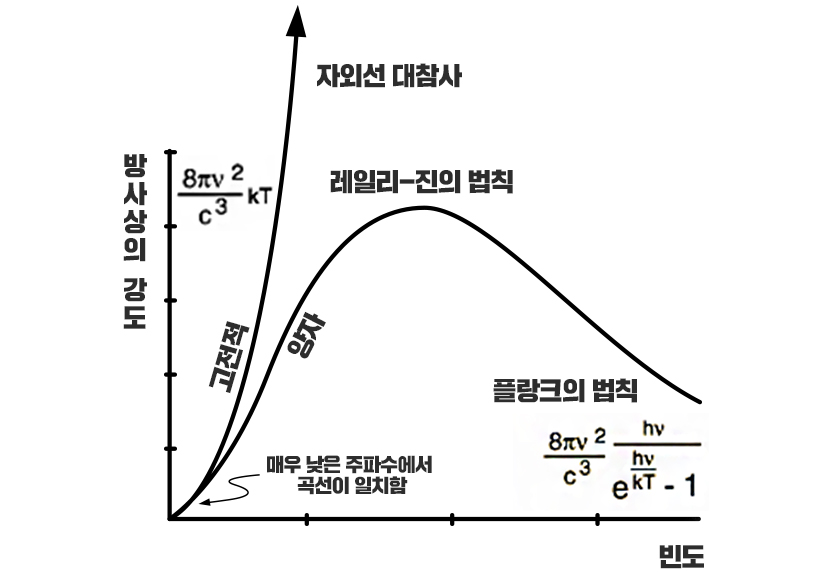▲ 흑체복사에 관한 고전역학과 양자역학 해석 비교

고전물리학에 의하면 에너지는 파동의 진폭(A2)에 비례하고 파장이 짧을수록 그 에너지가 크다고 생각하였다. 플랑크의 가설에서는 복사에너지의 크기를 나타내는 변수는 진폭에서 n(정수배)과 ν(진동수)로 대체된다. 그는 불연속적인 에너지 준위라는 개념을 통계역학적 해석과 접목하여 그가 구한 공식이 맞는지 증명하고자 하였다. 어떤 일정한 에너지 준위(불연속)가 일정한 시간 동안 발생한 횟수를 맥스웰-볼츠만 분포식으로 계산하였을 때, 놀랍게도 플랑크의 열복사식이 최종식으로 나왔다. 그 바탕에는 에너지는 nhν의 값 형태로 양자화되어 있다는 것이었다. 이로써 플랑크의 에너지 양자화 개념은 흑체복사에 있어서 반드시 필요한 개념이 되었으며, 양자역학의 서문을 연 계기가 되었다.

양자화 개념의 확대

플랑크 상수를 이용한 양자화 개념은 이후 광전효과 등을 비롯한 에너지의 불연속적인 특징을 지닌 빛의 입자성 해석에 활용되었다. 광전효과를 설명한 아인슈타인의 해석에 불만을 지닌 일부 연구자는 고전역학 관점에서 일함수의 개념을 부정하고자 하였는데, 밀리컨(Milikan)은 아인슈타인의 해석이 틀렸다고 생각하고 이를 증명하기 위해 10년간 반복실험을 했다. 진동수를 변화(⊿ν)시켜가면서 광전자 발생으로 인한 에너지 편차(⊿E)를 2차원 좌표로 나타내는 실험이었다. 결론은 늘 직선이 나타났다.

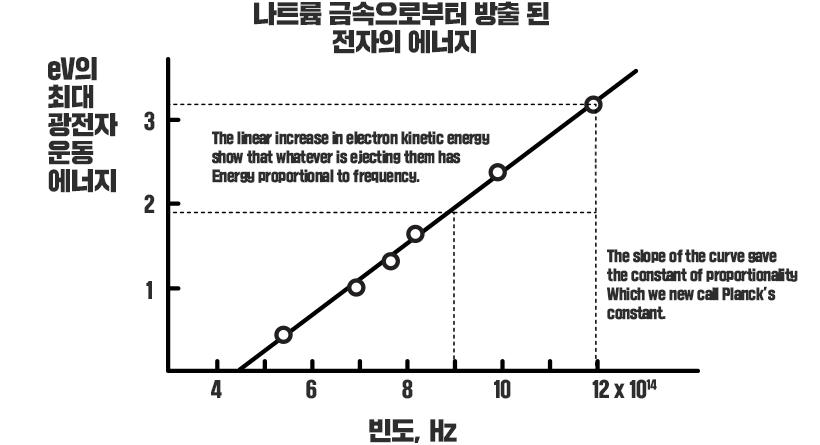
▲ 밀리컨의 플랑크 상수 계산 곡선

그 직선의 기울기(⊿E/⊿ν)가 의미하는 바가 바로 플랑크 상수인 h를 나타내는 것이었다. 현재의 값과 약 1%의 오차밖에 없을 정도로 정교한 실험이었다. 그는 고전물리학에 따라 문제를 해석하려고 하였으나, 역설적으로 에너지가 양자화되어있다는 플랑크의 중요 상수값을 자신의 실험으로 증명하게 된 셈이었다.

플랑크는 사실 양자론의 출발점에 있어서 상당히 중요한 인물이긴 하지만 전적으로 고전물리학에 갇혀 있었던 인물로 자신이 발견한 양자화된 에너지 상태를 믿고 싶어 하지 않았다. 하지만 그의 이론이 양자역학에 중요한 기초이자 발전의 토대가 된 것은 분명하다