
유체란 고체와 달리 외부의 작은 힘(전단응력)에도 견디지 못하고 쉽게 변형되면서 움직이는 액체나 기체 상태를 말합니다. 유체역학(流體力學, fluid dynamics)은 유체의 유동 현상을 다루며, 다양한 분야에서 응용되고 있습니다. 그럼 이제부터 유체역학에 대해 살펴보겠습니다.
일정한 형체를 갖지 않는 ‘유체’
우리 주변에서 회오리와 태풍 그리고 바닷물의 순환과 같은 자연현상을 쉽게 발견할 수 있습니다. 이처럼 주변에서 쉽게 찾아볼 수 있는 유체는 일정한 형체를 갖지 않고 흐름이 불규칙적이며 눈에 잘 보이지 않습니다. 이러한 성질로 유체는 이해하기 어렵고 신비한 것으로 여겨져 왔으며, 지금까지도 도전해 볼 만한 분야로 남아 있습니다.

과거 레오나르도 다빈치는 다양한 유체 흐름에 관심을 가지고 사실적인 와류 그림들을 여럿 남겼습니다. 또 데카르트는 보텍스 이론을 이용하여 우주의 기원을 와류현상으로 설명하고자 하였습니다. 보텍스 이론이란 미세한 소용돌이가 최소 단위를 이루고 이들이 모여 커다란 유체의 움직임을 구성한다고 보는 이론입니다.
정수력과 부력만 다루는 ‘유체 정역학’
 ▲ 유레카를 외치는 아르키메데스
▲ 유레카를 외치는 아르키메데스
유체역학 중에서 정지된 상태를 다루는 것을 유체 정역학(hydrostatics)이라 합니다. 움직임이 없기 때문에 단순히 정수력과 부력만을 다루면 됩니다. 과거 아르키메데스는 왕으로부터 금관에 은이 섞여 있는지를 판별하라는 명령을 받았습니다. 한참 고민 끝에 피곤한 몸으로 목욕탕에 갔다가 목욕탕 수조의 물이 넘치는 것을 보고 비중의 원리를 깨달았고, 옷도 걸치지 않은 상태로 ‘유레카’를 외쳤습니다. 물체가 받는 부력은 그 물체가 밀어낸 물의 무게와 같다는 원리를 발견하고, 이를 이용하여 물속과 물 밖에서 잰 금관의 무게로부터 밀도를 계산하고 위조된 금관을 판별할 수 있었습니다.
움직임을 다루는 ‘유체 동역학’
유체역학은 대개 움직임을 다루는 유체 동역학을 의미합니다. 유체 흐름은 유체에 작용하는 힘으로 발생합니다. 압력, 점성력, 중력 등 유체에 작용하는 힘을 모두 합하면 뉴턴의 법칙에 따라 가속도를 구할 수 있습니다. 하지만 측정이 어려운 데 그 이유는 유체가 물체 덩어리와 달리 질량 경계, 즉 시스템(system)이 명확하지 않기 때문입니다.
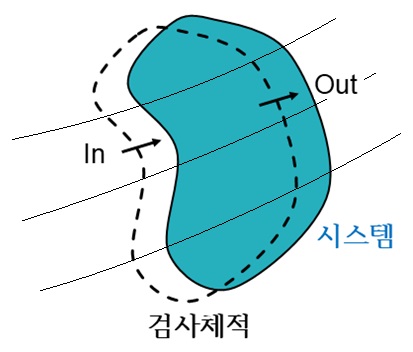
▲ 검사체적과 시스템
※ 검사체적 : 시간에 따라 부피는 변하지 않으나 질량, 운동량, 에너지 등의 물리량은 유동적인 가상의 체적(부피)
유체는 경계가 명확하지 않기 때문에 우리에게 익숙한 라그랑주(Lagrange) 관찰법을 쓸 수 없습니다. 라그랑주 관찰법이란 자동차나 비행기처럼 대상이 분명할 때, 그 대상을 따라가며 위치나 속도의 변화 등을 관찰하는 방법입니다. 하지만 유체의 경우는 흘러가면서 섞이고 흩어지기 때문에 관찰 대상을 명확히 특정 지을 수 없습니다.
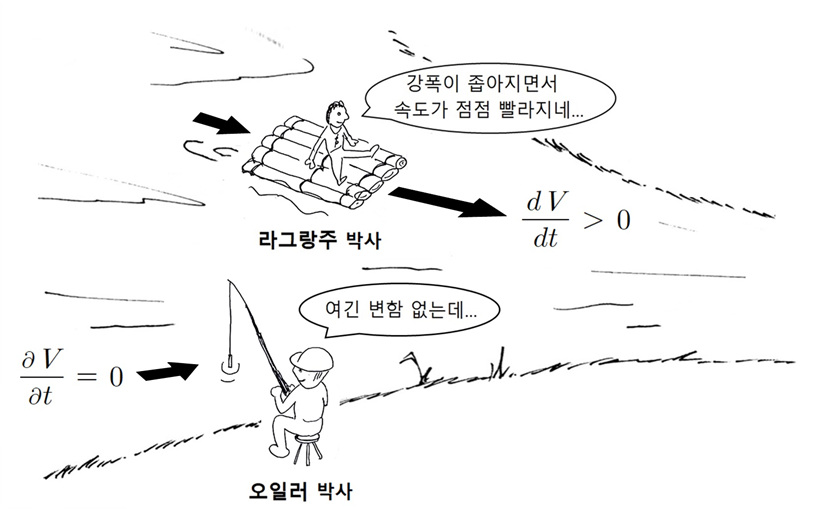 ▲ 좁아지는 수로에서 라그랑주와 오일러 관찰법에 따른 속도측정의 차이
▲ 좁아지는 수로에서 라그랑주와 오일러 관찰법에 따른 속도측정의 차이
그러므로 따라가면서 관찰하는 대신, 공간상에 고정된 지점 또는 그물망과 같은 검사체적을 쳐 놓고 지나는 대상들을 관찰해야 합니다. 이것을 오일러(Euler) 관찰법이라 합니다. 예를 들어 풍속을 측정한다고 할 때, 공기 입자를 따라가면서 잴 수 없어 풍속계를 고정하고 그 지점을 지나는 불특정 다수의 공기 입자들을 재는 것입니다. 또 한강 다리에 설치된 교통 카메라도 특정 자동차를 추적하는 것이 아닌 오일러 관찰법에 따라 그 지점을 통과하는 불특정 다수의 차량을 관찰하는 것입니다.
동압과 정압의 반비례, 베르누이 원리
유체역학 원리 중 가장 널리 알려진 것은 베르누이(Bernoulli) 정리입니다. 점성이 없는 유체의 경우에 정압과 동압의 합은 일정하다는 원리로 에너지 보존법칙과도 일맥상통합니다. 여기서 정압은 유체 자체가 가진 압력에 해당하며, 동압은 유체의 운동에너지가 압력 형태로 나타난 것입니다.
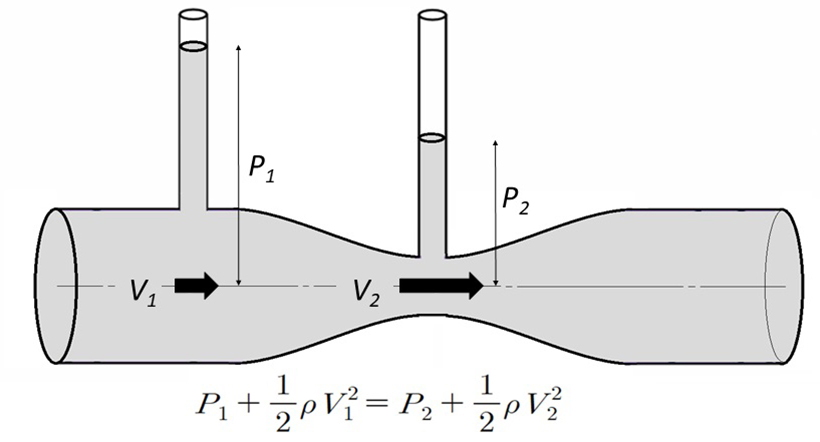 ▲ 좁은 목을 통과할 때 유체의 속도(동압)는 커지고 압력(정압)은 낮아진다.
▲ 좁은 목을 통과할 때 유체의 속도(동압)는 커지고 압력(정압)은 낮아진다.
베르누이 원리는 속도가 빠른 곳에서는 동압이 높아지고 정압이 낮아지며, 속도가 느린 곳에서는 동압이 낮아지고 정압이 높아지는 현상을 설명합니다. 예를 들어, 터널을 통과할 때 달리는 열차의 속도에 의해 열차 내 기압이 내려가 귀가 먹먹해지는 현상이 발생하거나, 분무기에 의해 물이 스프레이로 분사되는 것으로 설명 할 수 있습니다.
베르누이 원리를 아래 그림에서처럼 빨대와 압력을 이용해 간단하게 실험 해 보겠습니다.
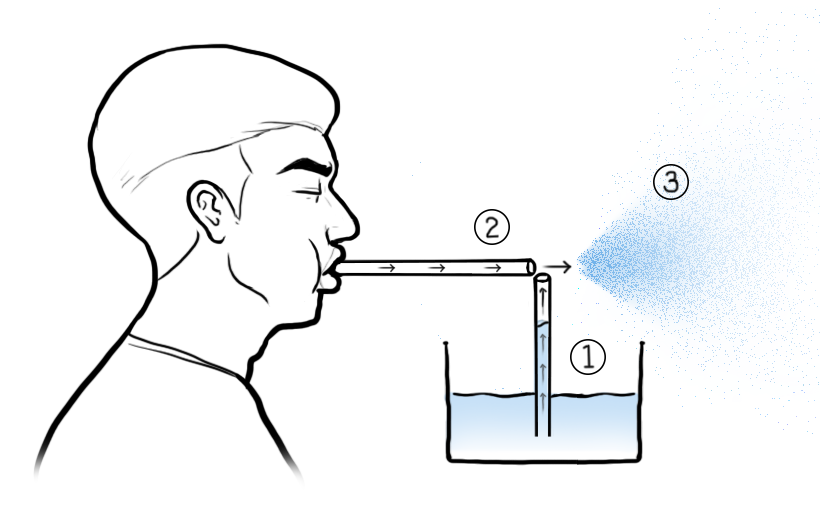
STEP 1. 물이 들어있는 수조 안에 빨대를 수직으로 세워놓으면 압력에 의해 물이 올라옵니다.
STEP 2. 수조에 세워진 빨대 상단 부분을 다른 빨대를 이용하여 바람을 붑니다.
STEP 3. 수조 안 빨대의 상단 부분은 압력이 낮아지면서 물이 올라와 스프레이처럼 분무됩니다.
그 외로 야구공을 회전시키면 커브볼이 되고, 비행기 날개에 양력이 발생하는 등 생활 속에서도 쉽게 베르누이 현상을 발견할 수 있습니다.
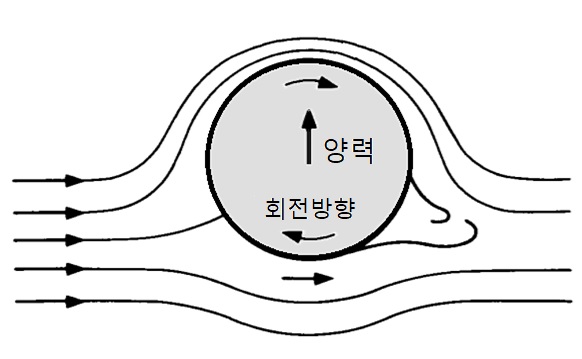
▲ 야구공 회전에 따른 베르누이 현상
속도의 제곱에 비례하는 ‘항력’
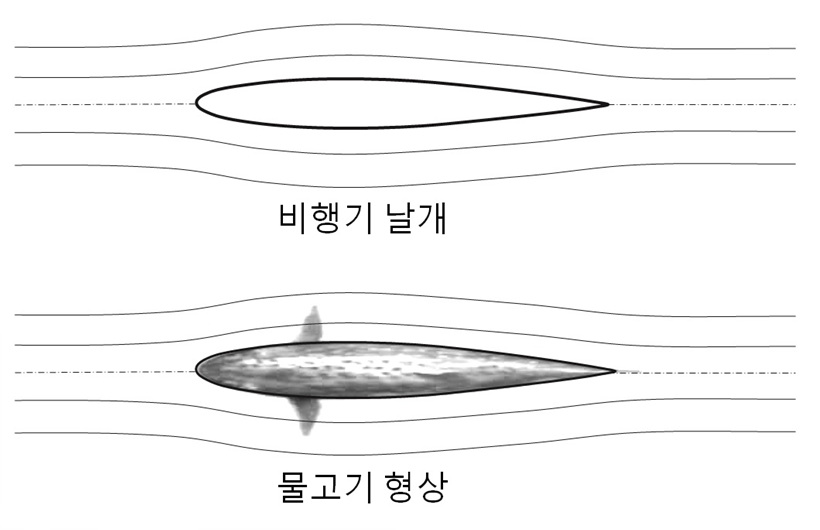
유체 중에서 이동하는 물체는 항력(drag)을 받습니다. 유체역학을 공부하는 목적 중의 하나는 항력을 계산하기 위한 것입니다. 일반적으로 항력은 속도의 제곱에 비례하기 때문에 속도가 빨라질수록 항력은 빠르게 증가합니다. 또 물체의 형상에 따라서 항력계수가 달라집니다.
고종 황제가 타던 자동차는 항력을 고려할 필요가 없었지만, 고속으로 달리는 스포츠카나 KTX는 공기항력이 매우 중요합니다. 항력계수를 줄이기 위해서 차체를 유선형으로 만들고 스포일러를 달아 유동 박리를 제어하는 등 다양한 방법을 사용합니다. 자전거 경기에서도 항력을 줄이기 위해 자전거를 날렵하게 만들어 항력계수를 줄이고, 선수는 최대한 몸을 웅크려 앞바람을 받는 면적을 줄여줍니다.
그런가 하면 골프공의 경우에는 특이한 박리 현상을 이용하여 항력계수를 줄입니다. 일반적으로는 거친 표면은 난류를 발생시키기 때문에 매끈한 표면보다 항력이 큽니다. 하지만 골프공의 경우는 울퉁불퉁한 표면 때문에 난류 박리점이 공의 뒤쪽으로 이동하면서 결과적으로 항력이 줄어드는 특이한 현상을 보입니다. 유체역학이 등장하기 이전부터 곰보 표면의 골프공이 멀리 날아간다는 사실은 경험적으로 잘 알려져 있었다고 합니다.
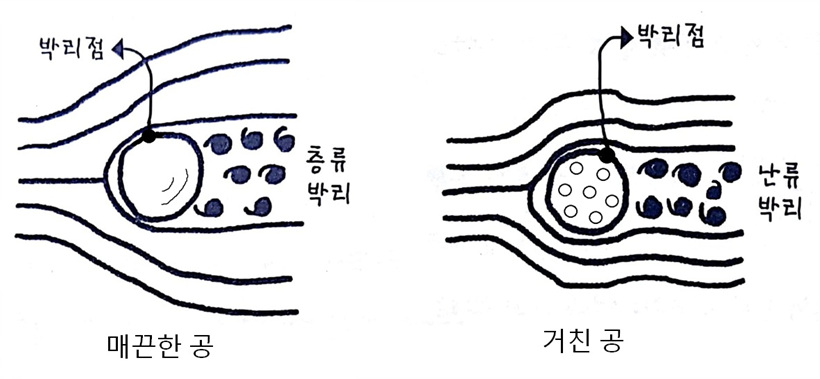 ▲ 매끈한 층류유동은 쉽게 박리되는데 비해, 거친 표면의 난류유동은 박리점이 하류쪽으로 물러나게 된다.
▲ 매끈한 층류유동은 쉽게 박리되는데 비해, 거친 표면의 난류유동은 박리점이 하류쪽으로 물러나게 된다.
반대로 유체 항력을 크게 하려는 경우도 있습니다. 낙하산의 항력계수를 가급적 크게 만들어 안전한 착지에 도움을 주며, 비행기가 활주로에 착륙할 때 날개를 위로 꺾어서 최대한의 항력을 유발시킵니다. 또한, 하늘에서 떨어지는 빗방울이 공기항력을 받아 안전하게 떨어진다는 사실이 얼마나 다행인지 모릅니다. 만일 항력이 없었다면 수km 상공에서 자유 낙하 하는 빗방울을 맞고 살아남을 사람은 없었을 것입니다. 비가 한 번 오면 땅바닥은 구멍투성이가 되고 농작물은 총알을 맞은 것처럼 온통 쑥대밭이 되고 말았을 것입니다.

유체역학은 20세기 세계대전을 겪으며 항공기를 개발하고 우주선을 쏴 올리면서 크게 발전하였습니다. 항공 분야에서는 주로 압축성 공기를 다루기 때문에 공기역학(aerodynamics)이라 하고, 조선이나 토목공학에서는 물을 다루기 때문에 수력학(hydrodynamics)이라 합니다. 최근에는 작은 스케일의 생체공학이나 마이크로 유체와 같은 새로운 분야에 널리 응용되고 있습니다. 또한, 기상학, 해양학, 생체역학 등 자연과학 분야에도 활발히 연구되고 있으며, 심지어 천체의 움직임이나 교통 흐름 등과 같이 유체가 아니더라도 다양한 흐름 현상을 해석하는 데에 적용하고 있습니다.

지금까지 유체역학에 대한 이야기를 나누었습니다.
이 세상에는 수많은 형태의 흐름이 있으며, 모두 유체역학의 원리와 연관 지어서 생각할 수 있을 것입니다. 공학의 기본 이론을 설명하는 ‘쉽게 알아보는 공학 이야기’ 다음 편도 기대해주세요.

